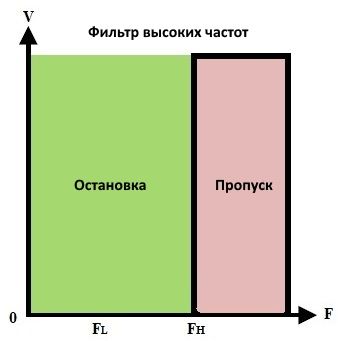
 Фильтр высоких частот пропускает частоты выше частоты среза и ослабляет частоты ниже частоты среза. В некоторых случаях этот фильтр называют фильтром низких частот или фильтром базовых частот. Величина ослабления или диапазон полосы пропускания будут зависеть от конструктивных параметров фильтра.
Фильтр высоких частот пропускает частоты выше частоты среза и ослабляет частоты ниже частоты среза. В некоторых случаях этот фильтр называют фильтром низких частот или фильтром базовых частот. Величина ослабления или диапазон полосы пропускания будут зависеть от конструктивных параметров фильтра.
Коэффициент усиления полосы пропускания активного фильтра превышает единичное усиление. Работа активного фильтра высоких частот такая же, как у пассивного фильтра высоких частот, но главное отличие состоит в том, что активный фильтр высоких частот использует операционный усилитель, который обеспечивает усиление выходных сигналов и регулирует усиление.
Идеальные характеристики фильтра высоких частот показаны ниже:
Вы должны помнить, что фильтр высоких частот пропускает частоты от точки среза частоты до частоты «бесконечности», которая не существует в практических соображениях. Помимо пассивного фильтра высоких частот, в этом активном фильтре высоких частот максимальная частотная характеристика ограничена характеристиками разомкнутого контура операционного усилителя.
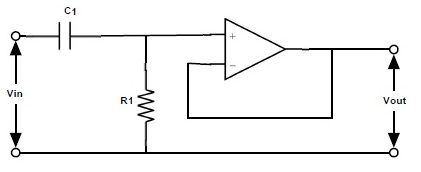
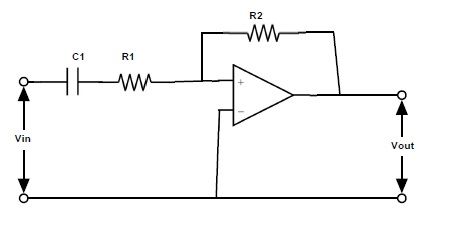
Цепь активного фильтра высоких частот
Подключив пассивную RC-цепь фильтра высоких частот к инвертирующему или неинвертирующему выводу операционного усилителя, мы получим активный фильтр высоких частот первого порядка. Схема пассивного RC-фильтра высоких частот, подключенная к неинвертирующему выводу операционного усилителя с единичным коэффициентом усиления, показана ниже:
Коэффициент усиления A max = 1 и частота среза f c = 1/2πRC
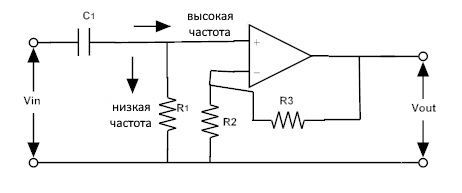
Активный фильтр высоких частот с усилением по высокому напряжению
Принцип работы такой же, как у пассивного фильтра высоких частот, но входной сигнал усиливается усилителем на выходе. Величина усиления зависит от коэффициента усиления усилителя.
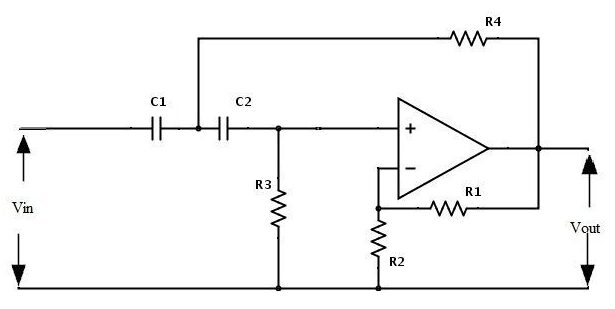
Величина усиления полосы пропускания равна 1 + (R 3 /R 2 ). Где R3 — резистор обратной связи в Ом, а R2 — входной резистор. Схема активного ФВЧ с усилением приведена ниже:
Усиление напряжения активного фильтра высоких частот
Коэффициент усиления по напряжению A v = A max (f / fc ) / √{1 + (f/fc)²}
Где, f = рабочая частота
fc = частота среза
A max = усиление полосы пропускания фильтра = 1 + (R 3 /R 2 )
На низких частотах, т.е. когда рабочая частота меньше частоты среза, коэффициент усиления по напряжению меньше коэффициента усиления полосы пропускания A max . На высоких частотах, т.е. когда рабочая частота больше частоты среза, коэффициент усиления фильтра по напряжению равен коэффициенту усиления полосы пропускания.
Если рабочая частота равна частоте среза, то коэффициент усиления фильтра по напряжению равен 0.707 Amax .
Усиление напряжения (дБ)
Величина усиления по напряжению обычно измеряется в децибелах (dB):
Av(dB) = 20 log10 (Vout/Vin)
-3 dB = 20 log10 (0.707 * Vout/Vin)
Частота среза, которая разделяет полосу пропускания и полосу задерживания, может быть рассчитана по приведенной ниже формуле:
fC = 1 / (2πRC)
Фазовый сдвиг активного фильтра высоких частот такой же, как у пассивного фильтра. Он равен +45° на частоте среза fC, а это значение фазового сдвига равно:
Ø = tan-1(1/2πfcRC)
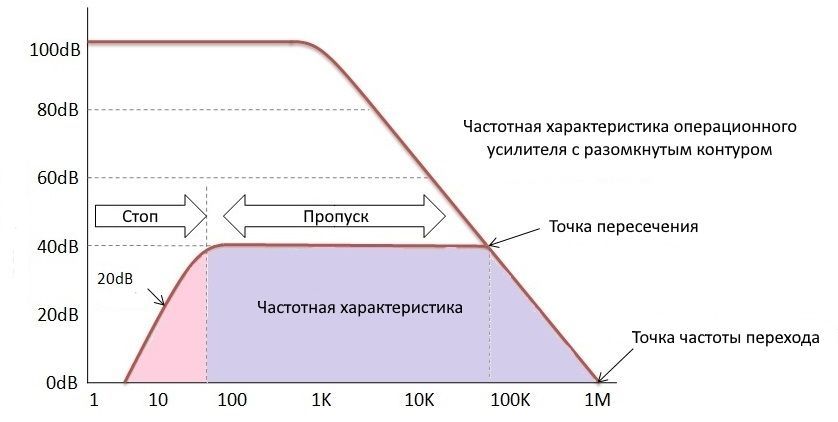
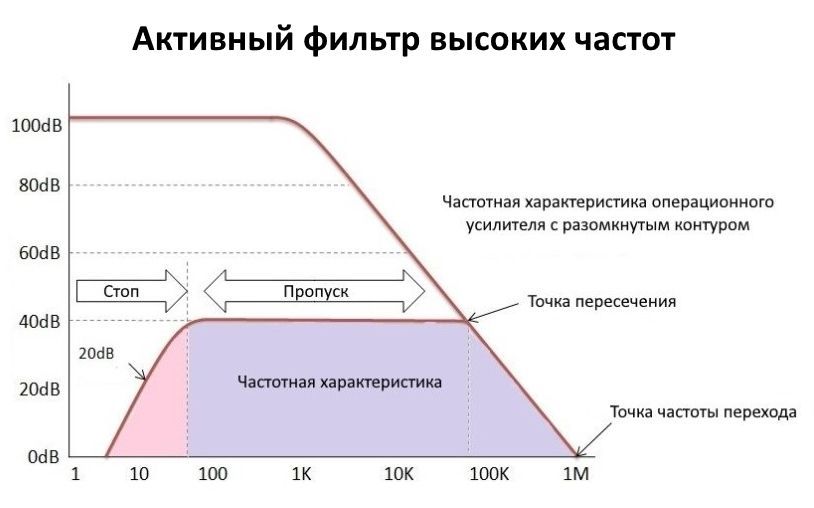
Частотная характеристика активного фильтра высоких частот
Кривая АЧХ по отношению к коэффициенту усиления разомкнутого контура усилителя показана ниже:
В частотной характеристике активного фильтра высоких частот максимальная частота полосы пропускания ограничена полосой пропускания или характеристиками разомкнутого контура операционного усилителя. Из-за этого ограничения отклика активного фильтра высоких частот будет похож на отклик широкополосного фильтра.
Используя этот активный фильтр высоких частот на основе операционного усилителя, мы можем достичь высокой точности с использованием резисторов и конденсаторов с малым допуском.
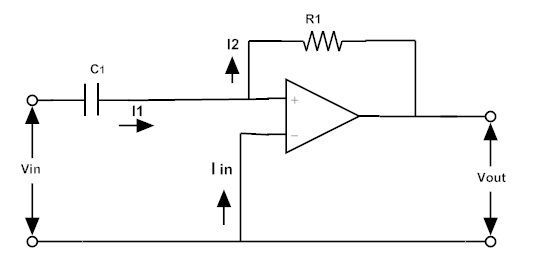
Активный фильтр высоких частот с использованием инвертирующего операционного усилителя
Вы должны помнить, что активный фильтр высоких частот может быть разработан с использованием либо инвертирующего, либо неинвертирующего вывода операционного усилителя. Давайте рассмотрим активный фильтр высоких частот с использованием инвертирующего операционного усилителя.
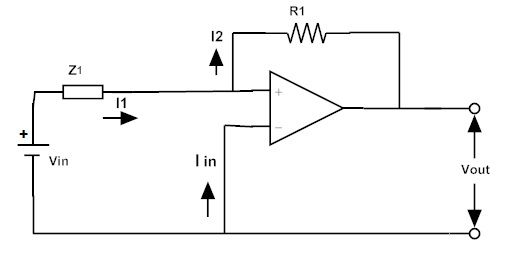
Вывод в форме Лапласа
Вот следующая схема инвертирующего усилителя:
Входное сопротивление Z1 = 1/sC1
Где, s = переменная Лапласа
C1 = емкость
В цепи протекают токи I1, I2 и Iin,
Где, I1 = I2 и Iin = 0
Vin / Z1 = -Vout / R1
Vout / Vin = – R1 / Z1
Vout / Vin = – R1 / (1/sC1)
Vout / Vin = -sR1C1 = Усиление
Пример активного фильтра высоких частот
Примем значение частоты среза 10 кГц, усиление полосы пропускания A max = 1,5 и значение конденсатора 0,02 мкФ.
Уравнение частоты среза:
f C = 1 / (2πRC)
Преобразовав это уравнение, мы получим:
R = 1 / (2πfC)
R = 1/(2π * 10000 * 0,02 * 10 -6 ) = 795,77 Ом
Коэффициент усиления полосы пропускания фильтра A max = 1 + (R 3 /R 2 ) = 1,5.
R3 = 0,5 R2
Если мы рассмотрим значение R2 как 10 кОм, то:
R3 = 5 кОм
Мы можем рассчитать усиление фильтра следующим образом — усиление напряжения для фильтра высоких частот:
| Vout / Vin | = Amax * (f/fc) /√[1 + (f/fc)²]
Av(dB) = 20 log10 (Vout/Vin)
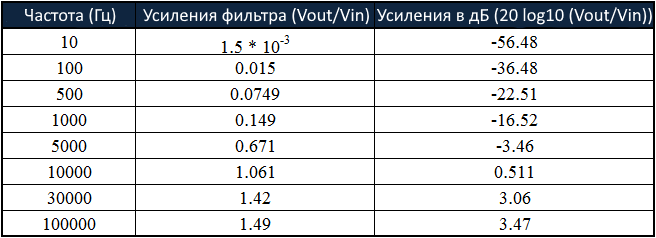
Используя это уравнение, давайте сведем в таблицу отклики для диапазона частот, чтобы построить кривую отклика фильтра. Предполагается, что эти отклики находятся в диапазоне от 10 Гц до 100 кГц:
График Боде
Для анализа частотной характеристики схемы используется этот график Боде. Это не что иное, как график линейной передаточной функции, изменяющейся во времени, в зависимости от частоты. График построен с логарифмической осью частоты. Он состоит в основном из двух участков; один — график величины, а другой — фазовый график.
График амплитуды будет выражать амплитуду частотной характеристики, т. е. усиление, а фазовый график используется для выражения отклика частотного сдвига.
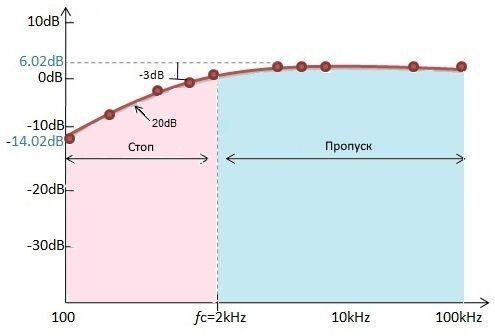
График частотной характеристики в соответствии со значениями, приведенными в таблице выше, приведен ниже:
Согласно рассчитанным значениям, на частоте 10 Гц коэффициент усиления фильтра, полученный в дБ, составляет -56,48. Если мы увеличим значение частоты до 100 Гц, то получим усиление -36,48 дБ, а на частоте 500 Гц усиление фильтра составит -22,51 дБ.
На частоте 1000 Гц коэффициент усиления в дБ составляет -16,52. Таким образом, мы можем сказать, что при увеличении частоты коэффициент усиления фильтра увеличивается со скоростью 20 дБ/декада.
До частоты среза 10 кГц коэффициент усиления фильтра увеличивается, но после частоты среза коэффициент усиления достигает максимального значения и остается постоянным.
Фильтр высоких частот второго порядка
Частотная характеристика активного фильтра второго порядка прямо противоположна характеристике активного фильтра низких частот второго порядка, потому что этот фильтр будет ослаблять напряжения ниже частоты среза. Передаточная функция фильтра второго порядка приведена ниже:
Vout(s) / Vin(s) = -Ks² / s² + (ω0/Q)s + ω0²
Где, K = R1/R2 and ω0 = 1/CR
Это общая форма фильтра высоких частот второго порядка.
Цепь активного фильтра высоких частот второго порядка
Процедура проектирования активного фильтра второго порядка такая же, как и у фильтра первого порядка, поскольку единственным отличием является спад. Если спад активного фильтра высоких частот первого порядка составляет 20 дБ/декада, то спад фильтра второго порядка составляет 40 дБ/декаду.
Это означает удвоение значения фильтра первого порядка. Схема фильтра второго порядка показана ниже:
Коэффициент усиления фильтра равен 1+ R1/R2, а уравнение частоты среза: f c = 1/ 2π√R 3 R 4 C 1 C 2
Пример активного фильтра высоких частот второго порядка
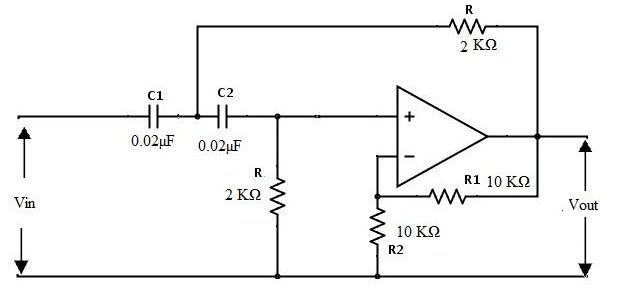
Разработаем фильтр с частотой среза 4 кГц и коэффициентом задержки в полосе задерживания 40 дБ/дек. Поскольку скорость задержки в полосе задерживания составляет 40 дБ/дек, мы можем однозначно сказать, что фильтр является фильтром второго порядка.
Рассмотрим номиналы конденсаторов как:
C1= C2 = C = 0,02 мкФ.
Уравнение частоты среза:
R = 1/2πfC
Преобразовав это уравнение, мы получим:
R = 1⁄2πfC
Заменив значения частоты среза на 4 кГц и конденсатора на 0,02 мкФ:
R = 1,989 кОм = 2 кОм
Пусть коэффициент усиления фильтра равен:
1+ R1/R2 = 2.
R1 / R2 = 1
Р1 = Р2
Поэтому можно взять:
R1 = R2 = 10 кОм
Таким образом, полученный фильтр показан ниже:
Фильтры высоких частот высокого порядка
Каскадируя фильтр первого порядка с фильтром второго порядка, мы можем получить фильтр третьего порядка. Когда мы каскадируем два фильтра второго порядка, мы можем получить фильтр четвертого порядка. Таким образом, с помощью фильтров первого и второго порядка мы получаем фильтры более высокого порядка.
С увеличением порядка фильтра разница между фактической полосой заграждения и теоретической полосой заграждения увеличивается. Но общий коэффициент усиления фильтра более высокого порядка одинаков, потому что резисторы и конденсаторы, определяющие значения частотной характеристики, будут одинаковыми.
Итог
Данные фильтры используются в громкоговорителях для уменьшения шума низкого уровня. Устраняет искажения грохота в аудиоприложениях, поэтому они также называются фильтрами повышения высоких частот. Фильтры используются в аудиоусилителях для усиления высокочастотных сигналов, а также используются в эквалайзерах.
В следующей статье мы с вами поговорим об активном полосовом фильтре.
С Уважением, МониторБанк