Блог

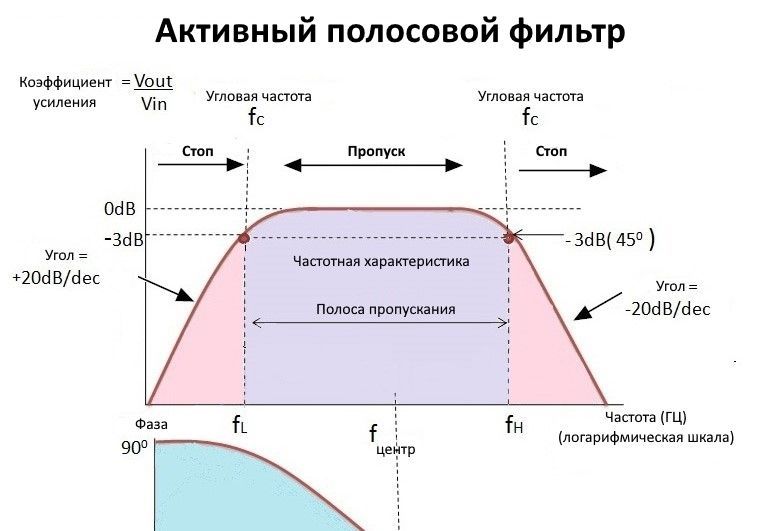
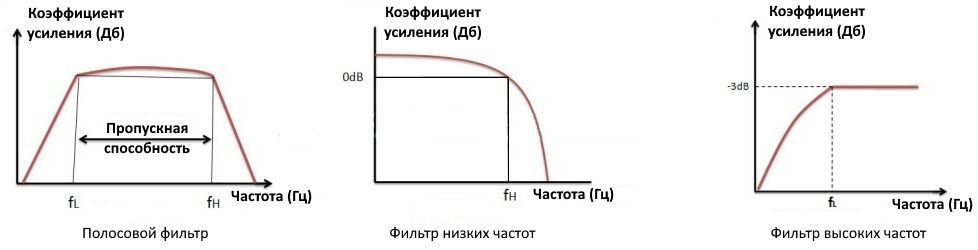
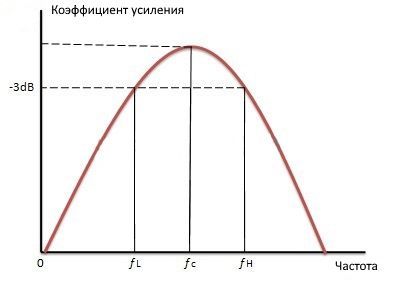
Полосовой фильтр — это схема, пропускающая через себя только определенную полосу частот. Эта полоса пропускания находится в основном между частотами среза, и они равны f_L  и f_H,  где f_L  — нижняя частота среза, а f_H  — более высокая частота среза.

Центральная частота обозначается буквой «f_C» и также называется резонансной частотой или пиковой частотой.

Значение f_L  всегда должно быть меньше значения f_H. Полоса пропускания фильтра — это не что иное, как полоса пропускания частот. Усиление фильтра максимально на резонансной или центральной частоте называется полным усилением полосы пропускания. Это усиление полосы пропускания обозначается как «A_max».

Для фильтра низких частот эта полоса пропускания начинается с 0 Гц и продолжается до тех пор, пока не достигнет значения резонансной частоты на -3 дБ ниже максимального усиления полосы пропускания.

При этом, как и в случае ФВЧ, эта полоса пропускания начинается с резонансной частоты -3 дБ и заканчивается на значении максимального усиления контура для активного фильтра. Комбинация низких и высоких частот дает нам полосовой отклик, как показано ниже:

Активный полосовой фильтр

В зависимости от добротности полосовой фильтр подразделяется на широкополосный фильтр и узкополосный фильтр. Каскадируя фильтр высоких частот и фильтр нижних частот с усиливающим компонентом, мы получим полосовой фильтр.

Цепь усилителя между этими фильтрами высоких и низких частот обеспечивает изоляцию и дает общий коэффициент усиления по напряжению в цепи. Значения частот среза обоих фильтров должны поддерживаться с минимальной разницей.

Если эта разница очень мала, может существовать возможность взаимодействия ступеней высоких и низких частот. Таким образом, чтобы получить надлежащие уровни этих частот среза, необходима схема усиления.

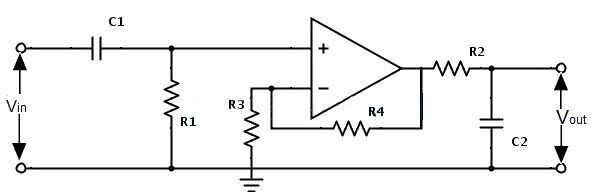
Принципиальная схема активного полосового фильтра показана ниже:

Широкополосный фильтр

Если значение добротности меньше десяти, то полоса пропускания широкая, что дает нам большую полосу пропускания. Этот полосовой фильтр называется широкополосным фильтром.

В этом фильтре верхняя частота среза должна быть больше нижней частоты среза. В конструкции используются два усилительных элемента (ОУ).

Сначала сигнал пройдет через фильтр высоких частот, выходной сигнал этого фильтра высоких частот будет стремиться к бесконечности, и, таким образом, сигнал, стремящийся к бесконечности, подается в фильтр низких частот в конце.

Этот фильтр низких частот пропускает высокочастотный сигнал.

Когда фильтр высоких частот каскадируется с фильтром низких частот, получается простой полосовой фильтр. Чтобы реализовать этот фильтр, порядок схем низких и высоких частот должен быть одинаковым.

Путем каскадирования одного фильтра низких частот первого порядка и фильтра высоких частот мы получаем полосовой фильтр второго порядка, а каскадирование двух фильтров низких частот первого порядка с двумя фильтрами высоких частот образует полосовой фильтр четвертого порядка.

Из-за такого каскадирования схема имеет низкое значение добротности. Конденсатор в фильтре высоких частот первого порядка будет блокировать любое смещение постоянного тока от входного сигнала.

Спад усиления на обеих полосах задерживания составляет ± 20 дБ/дек в случае фильтра второго порядка (высокий + низкий). Фильтры высоких и низких частот должны быть только первого порядка.

Точно так же, когда фильтры высоких и низких частот имеют второй порядок, спад усиления на обеих полосах задерживания составляет ± 40 дБ/дек.

Выражение усиления по напряжению для полосового фильтра имеет вид:

| V_out / V_in | = [A_max * (f/f_L)] / √{[1+(f/f_L)²][1+(f/f_H)²]}

Так получается с помощью отдельных коэффициентов усиления фильтров высоких и низких частот, индивидуальные коэффициенты усиления фильтров высоких и низких частот приведены ниже.

Усиление напряжения для фильтра высоких частот:

| V_out / V_in | = [A_max1 * (f/f_L)] / √[1+(f/f_L)²]

Усиление напряжения для фильтра низких частот:

| V_out / V_in | = A_max2 / √[1+(f/f_H)²]

A_max = A_max1 * A_max2

Где, A max1 — усиление каскада высоких частот, а A max2 — усиление каскада низких частот.

Отклик широкополосного фильтра показан ниже:

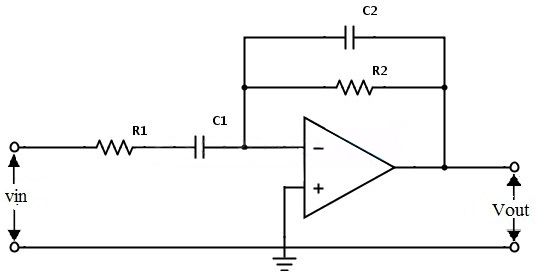
Узкополосный фильтр

Если значение добротности больше десяти, то полоса пропускания узкая и ширина полосы пропускания также меньше. Этот полосовой фильтр называется узкополосным фильтром.

Он использует только один активный компонент (операционный усилитель), а не два, и этот операционный усилитель находится в инвертирующей конфигурации. В этом фильтре коэффициент усиления операционного усилителя максимален на центральной частоте fc .

Цепь узкополосного фильтра

Вход подается на инвертирующий входной терминал. Это показывает, что операционный усилитель находится в инвертирующей конфигурации. Приведенная ниже схема фильтра обеспечивает отклик узкополосного фильтра:

Коэффициент усиления по напряжению приведенной выше схемы фильтра равен A _V = – R ₂ / R ₁ 

Частоты среза схемы фильтра:

f _C1 = 1 / (2πR ₁ C ₁ ) и f _C2 = 1 / (2πR ₂ C ₂ )

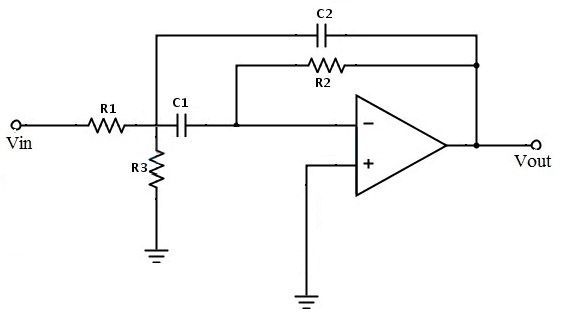
Активный полосовой фильтр с множественной обратной связью

Эта схема фильтра создает настроенную схему на основе отрицательной обратной связи фильтра. Важным преимуществом этой многократной обратной связи является то, что без какого-либо изменения максимального усиления на центральной частоте мы можем изменить значение частоты среза. Это изменение частоты среза может быть выполнено сопротивлением R3 .

Рассматривая приведенную ниже схему активного фильтра, давайте рассмотрим измененное значение резистора как R3′ и измененное значение частоты среза как f c’, тогда мы можем приравнять для нового значения резистора следующим образом:

R ₃ ′ = R ₃ (f _c /f _c ′)²

Схема состоит из двух путей обратной связи, из-за этого множества путей обратной связи она называется «схемой с множественной обратной связью». Эта схема создает полосовой фильтр с множественной обратной связью с бесконечным усилением. За счет этой схемы значение добротности увеличивается максимально до 20.

f_c = 1/√(R₁R₂C₁C₂)

Q = f_c/Пропускная способность = (½){√[R₂/R₁]}

A_max = -R₂/2R₁

R₁ = Q/{2πf_cCA_max}

R₂ = Q/πf_cC

R₃ = Q/{2πf_cC(2Q² – A_max)}

Коэффициент усиления на центральной частоте «A max» должен быть меньше 2Q². То есть, Максимум < 2Q².

Где,

fc = частота среза в Гц
C = емкость, (C 1 = C 2 = C)
Q = добротность
A max = максимальное усиление

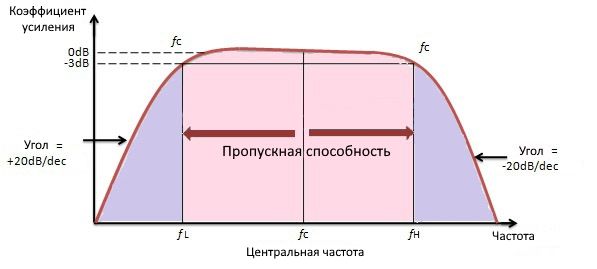
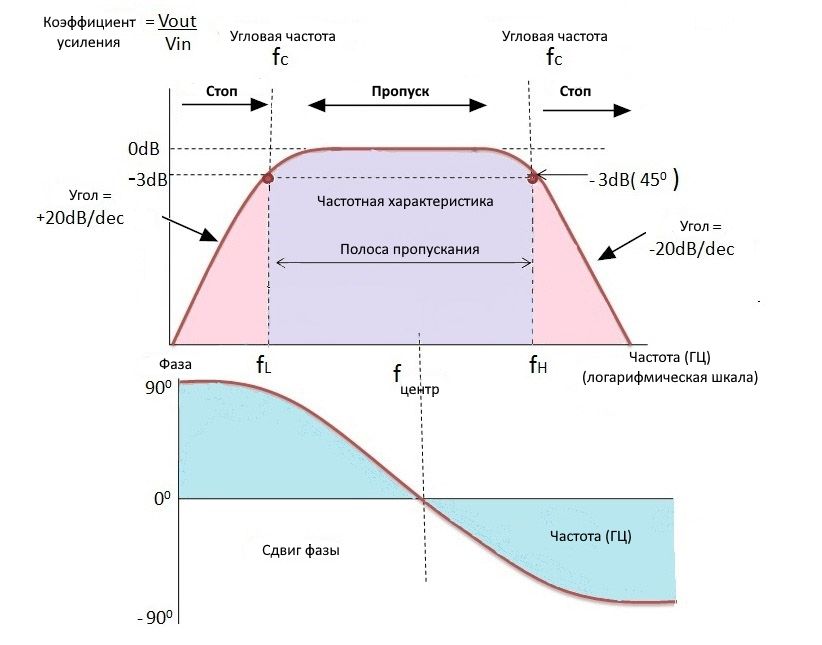
Частотная характеристика активного полосового фильтра

Он имеет две центральные частоты, одна для фильтра высоких частот, а другая для фильтра низких частот. Центральная частота фильтра высоких частот должна быть ниже центральной частоты фильтра низких частот.

Центральная частота полосового фильтра представляет собой среднее геометрическое низкой и высокой частот среза f r 2 = f H * f L.

Усиление фильтра составляет 20 log (V out / V in ) дБ/дек. Амплитудная характеристика аналогична характеристикам фильтра низких и высоких частот. В зависимости от порядка каскадного фильтра зависит кривая отклика.

Нормализованная средняя частота задается как fr = 1. Рассмотрим две частоты среза как 300 Гц и 900 Гц, тогда полоса пропускания фильтра составляет 300 Гц -900 Гц = 600 Гц.

Фактор качества

Коэффициент качества зависит от ширины полосы пропускания. Коэффициент качества обратно пропорционален пропускной способности. Это означает, что если ширина полосы увеличивается, коэффициент качества уменьшается, а если ширина полосы уменьшается, коэффициент качества увеличивается.

Q = f _c / полоса пропускания

Для широкополосного фильтра добротность низкая из-за большой ширины полосы пропускания. Для узкополосного фильтра добротность высока. Селективность и неселективность зависят от ширины полосы пропускания.

Этот коэффициент качества также относится к коэффициенту демпфирования (). Чем больше значение коэффициента демпфирования, тем больше неравномерность выходного отклика. Это показано следующим образом:

ε = 2/Q

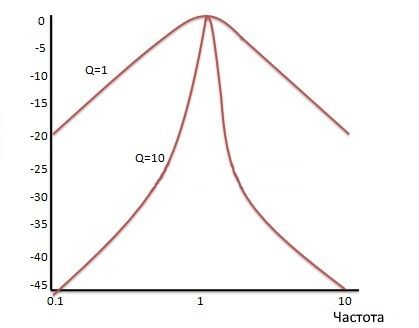
Для различных значений коэффициента качества нормализованная характеристика усиления полосового фильтра второго порядка задается как:

По этому графику видно, что, чем выше добротность, тем выше селективность.

Пример активного полосового фильтра

Рассмотрим схему активного фильтра с множественной обратной связью с бесконечным усилением, для которой резонансная частота составляет 1,5 кГц, максимальное усиление по напряжению равно 15, а добротность равна 7. Затем значения компонентов рассчитываются следующим образом:

Для резисторов:

Мы считаем, что измененное значение резистора как R 3 ´ и измененное значение частоты среза f c ´=2 кГц, тогда мы можем приравнять для нового значения резистора следующим образом:

R ₃ ´ = R ₃ (f _c /f _c ´) ² = 447,4(1,5/2) ² = 251,66 Ом

Поэтому, просто взяв требуемую частоту, мы можем рассчитать новое значение резистора.

В следующей статье мы поговорим о фильтре Баттерворта.

С Уважением, МониторБанк