Двоичное или бинарное дерево поиска или BST, как его обычно называют, представляет собой двоичное дерево, которое подходит под следующие условия:
Двоичное или бинарное дерево поиска или BST, как его обычно называют, представляет собой двоичное дерево, которое подходит под следующие условия:
- Узлы, которые меньше корневого узла, который помещается как левый дочерний элемент BST.
- Узлы, которые больше, чем корневой узел, размещенный как правый дочерний элемент BST.
- Левое и правое поддеревья, в свою очередь, являются бинарными деревьями поиска.
Такое расположение ключей в определенной последовательности помогает программисту более эффективно выполнять такие операции, как поиск, вставка, удаление и т.д. Если узлы не упорядочены, нам может потребоваться сравнить каждый узел, прежде чем мы сможем получить результат операции.
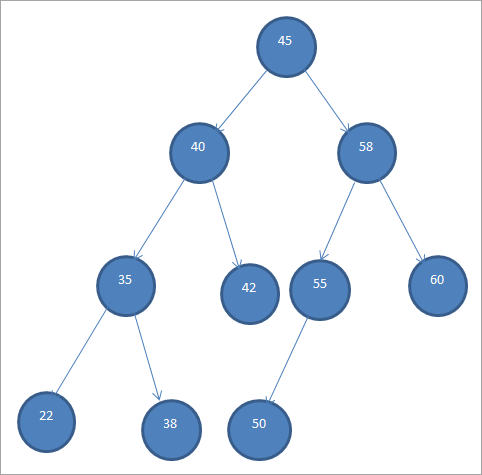
Пример BST показан ниже:
Бинарные деревья поиска также называют «упорядоченными двоичными деревьями» из-за такого особого порядка узлов.
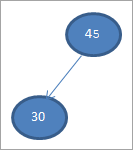
Из приведенного выше BST видно, что в левом поддереве есть узлы меньше корня, то есть 45, а в правом поддереве есть узлы больше 45.
Теперь давайте обсудим некоторые основные операции BST.
Основные операции
1) Вставка
Операция вставки добавляет новый узел в бинарное дерево поиска.
Алгоритм операции вставки бинарного дерева поиска приведен ниже:
|
1 2 3 4 5 6 7 8 9 10 |
Insert(data) Begin If node == null Return createNode(data) If(data >root->data) Node->right = insert(node->left,data) Else If(data < root->data) Node->right = insert(node>right,data) Return node; end |
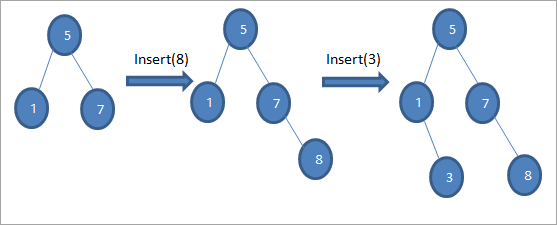
Как показано в приведенном выше алгоритме, мы должны убедиться, что узел размещен в соответствующей позиции, чтобы не нарушать порядок BST:
В приведенной выше на схеме последовательности, мы делаем ряд операций вставки. После сравнения вставляемого ключа с корневым узлом выбирается левое или правое поддерево для ключа, который будет вставлен в качестве листового узла в соответствующей позиции.
2) Удаление
Операция удаления удаляет узел, соответствующий данному ключу, из BST. В этой операции мы также должны изменить положение оставшихся узлов после удаления, чтобы порядок BST не нарушался.
Следовательно, в зависимости от того, какой узел мы должны удалить, у нас есть следующие случаи удаления в BST:
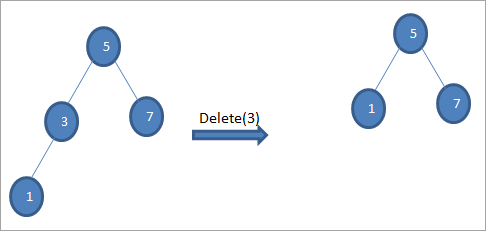
1) Когда узел является конечным узлом
Когда удаляемый узел является конечным узлом, мы удаляем узел напрямую:
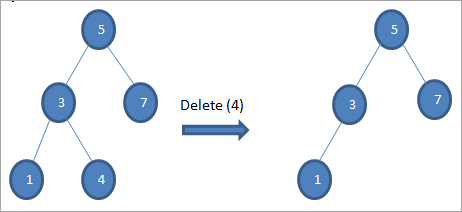
2) Когда у узла есть только один дочерний элемент
Когда у удаляемого узла есть только один дочерний узел, мы копируем дочерний узел и удаляем дочерний узел:
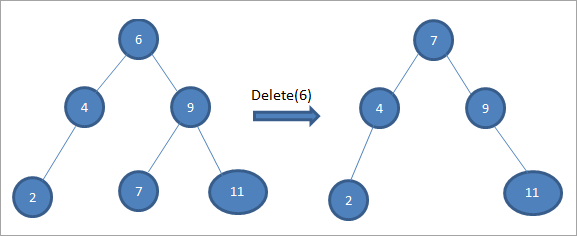
3) Когда у узла есть два потомка — преемника
Если удаляемый узел имеет двух дочерних элементов, то мы находим неупорядоченный преемник для узла, а затем копируем неупорядоченный преемник в узел. Позже мы удаляем преемника по порядку:
В приведенном выше дереве, чтобы удалить узел 6 с двумя дочерними элементами, мы сначала находим потомка по порядку для этого удаляемого узла. Мы находим преемника по порядку, находя минимальное значение в правом поддереве. В приведенном выше случае минимальное значение равно 7 в правом поддереве. Мы копируем его в удаляемый узел, а затем удаляем преемника по порядку.
3) Поиск
Операция поиска BST ищет конкретный элемент, идентифицированный как «ключ» в BST. Преимущество поиска элемента в BST состоит в том, что нам не нужно искать все дерево. Вместо этого из-за порядка в BST мы просто сравниваем ключ с корнем.
Если ключ совпадает с root, то мы возвращаем root. Если ключ не является корневым, то мы сравниваем его с корнем, чтобы определить, нужно ли искать в левом или правом поддереве. Как только мы находим поддерево, нам нужно найти ключ, и мы рекурсивно ищем его в любом из поддеревьев.
Ниже приведен алгоритм операции поиска в BST:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Search(key) Begin If(root == null || root->data == key) Return root; If(root->key < key) Search(root->left,key) Else if (root->key >key ) Search(root->right,key); end |
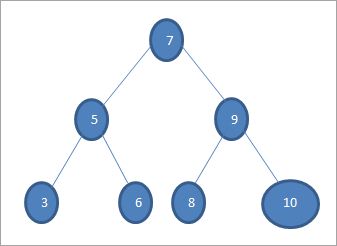
Если мы хотим найти ключ со значением 6 в приведенном выше дереве, то сначала мы сравниваем ключ с корневым узлом, т.е. если (6==7) => Нет, если (6<7) =Да; это означает, что мы будем опускать правое поддерево и искать ключ в левом поддереве.
Далее спускаемся к левому поддереву. Если (6 == 5) => Нет.
Если (6 < 5) => Нет; это означает, что 6>5, и мы должны двигаться вправо.
Если (6==6) => Да; ключ найден.
4) Обходы
Мы уже обсуждали обходы бинарного дерева. В случае BST мы также можем пройти по дереву, чтобы получить последовательность inOrder, preorder или postOrder. Фактически, когда мы проходим BST в последовательности Inorder01, мы получаем отсортированную последовательность:
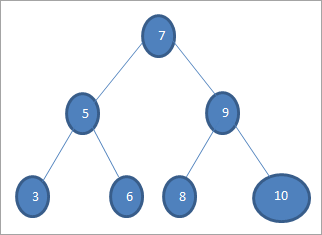
Обходы для вышеуказанного дерева следующие:
- Обход в порядке (lnr): 3 5 6 7 8 9 10
- Обход в предварительном порядке (nlr): 7 5 3 6 9 8 10
- Обход после заказа (lrn): 3 6 5 8 10 9 7
Демонстрация
Давайте создадим бинарное дерево поиска из данных, приведенных ниже.
45 30 60 65 70
Возьмем первый элемент в качестве корневого узла.
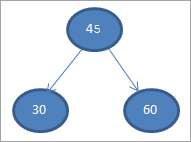
№1) 45
На последующих шагах мы будем размещать данные в соответствии с определением дерева бинарного поиска, т.е. если данные меньше, чем родительский узел, то они будут помещены в левый дочерний узел, а если данные больше, чем родительский узел, то они будут правым дочерним узлом.
Эти шаги показаны ниже.
2) 30
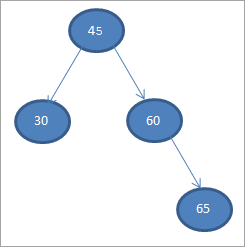
3) 60
4) 65
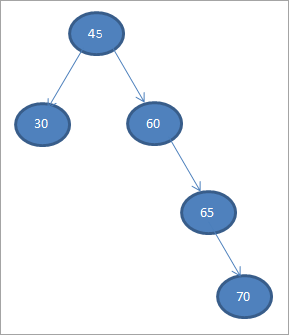
5) 70
Когда мы выполняем неупорядоченный обход только что созданного BST, последовательность действий следующая:
Теперь видно, что последовательность обхода имеет элементы, расположенные в порядке возрастания:
Реализация бинарного дерева поиска C++
Давайте рассмотрим BST и его операции, используя реализацию C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 |
#include<iostream> using namespace std; //объявление для нового узла bst struct bstnode { int data; struct bstnode *left, *right; }; // создать новый узел BST struct bstnode *newNode(int key) { struct bstnode *temp = new struct bstnode(); temp->data = key; temp->left = temp->right = NULL; return temp; } // выполнить неупорядоченный обход BST void inorder(struct bstnode *root) { if (root != NULL) { inorder(root->left); cout<<root->data<<" "; inorder(root->right); } } /* вставить новый узел в BST с заданным ключом */ struct bstnode* insert(struct bstnode* node, int key) { //дерево пусто; вернуть новый узел if (node == NULL) return newNode(key); //если дерево не пусто, найдите подходящее место для вставки нового узла if (key < node->data) node->left = insert(node->left, key); else node->right = insert(node->right, key); //вернуть указатель узла return node; } //возвращает узел с минимальным значением struct bstnode * minValueNode(struct bstnode* node) { struct bstnode* current = node; //искать самое левое дерево while (current && current->left != NULL) current = current->left; return current; } //функция для удаления узла с заданным ключом и перестановкой корня struct bstnode* deleteNode(struct bstnode* root, int key) { // пустое дерево if (root == NULL) return root; // поиск по дереву и если ключ < корень к крайнему левому дереву if (key < root->data) root->left = deleteNode(root->left, key); // если ключ > корень к самому правому дереву else if (key > root->data) root->right = deleteNode(root->right, key); // ключ такой же, как корень else { // узел только с одним дочерним элементом или без дочернего элемента if (root->left == NULL) { struct bstnode *temp = root->right; free(root); return temp; } else if (root->right == NULL) { struct bstnode *temp = root->left; free(root); return temp; } // узел с обоими дочерними элементами; получить потомка, а затем удалить узел struct bstnode* temp = minValueNode(root->right); // Скопируйте содержимое потомка в этом узле root->data = temp->data; // Удалить потомка по порядку root->right = deleteNode(root->right, temp->data); } return root; } // основная программа int main() { /* создадим следующий BST 40 / \ 30 60 \ 65 \ 70*/ struct bstnode *root = NULL; root = insert(root, 40); root = insert(root, 30); root = insert(root, 60); root = insert(root, 65); root = insert(root, 70); cout<<"Binary Search Tree created (Inorder traversal):"<<endl; inorder(root); cout<<"\nDelete node 40\n"; root = deleteNode(root, 40); cout<<"Inorder traversal for the modified Binary Search Tree:"<<endl; inorder(root); return 0; } |
Вывод данных:
| Создано бинарное дерево поиска (обход в порядке): 30 40 60 65 70 Удалить узел 40 Неупорядоченный обход модифицированного бинарного дерева поиска: 30 60 65 70 |
В приведенной выше программе мы выводим BST для последовательного обхода по порядку.
Преимущества BST
1) Поиск очень эффективен
У нас есть все узлы BST в определенном порядке, поэтому поиск определенного элемента очень эффективен. Так происходит потому, что нам не нужно искать все дерево и сравнивать все узлы.
Нам просто нужно сравнить корневой узел с элементом, который мы ищем, а затем мы решаем, нужно ли нам искать в левом или правом поддереве.
2) Эффективная работа по сравнению с массивами и связными списками
Когда мы ищем элемент в случае BST, мы избавляемся от половины левого или правого поддерева на каждом шаге, тем самым улучшая производительность операции поиска. Такой поиск отличается от массивов или связных списков, в которых нам нужно последовательно сравнивать все элементы для поиска определенного элемента.
3) Быстрая вставка и удаление
Операции вставки и удаления также выполняются быстрее по сравнению с другими структурами данных, такими как связные списки и массивы.
Применения BST
Вот некоторые из основных применений BST:
- BST используется для реализации многоуровневого индексирования в приложениях баз данных.
- BST также используется для реализации таких приложений, как словари.
- BST можно использовать для реализации различных эффективных алгоритмов поиска.
- BST также используется в приложениях, которым требуется отсортированный список в качестве входных данных, таких как интернет-магазины.
Итог
Бинарные деревья поиска (BST) представляют собой вариант двоичного дерева и широко используются в области программного обеспечения. Их также называют упорядоченными бинарными деревьями, поскольку каждый узел в BST размещается в определенном порядке.
Неупорядоченный обход BST дает нам отсортированную последовательность элементов в порядке возрастания. Когда для поиска используются BST, то поиск происходит очень эффективно и выполняется в кратчайшие сроки. BST также используются в кодировании Хаффмана, многоуровневых индексаций в базах данных и т. д.
В следующей нашей статье мы поговорим о деревьях AVL и структурах данных кучи в C++.
С Уважением, МониторБанк