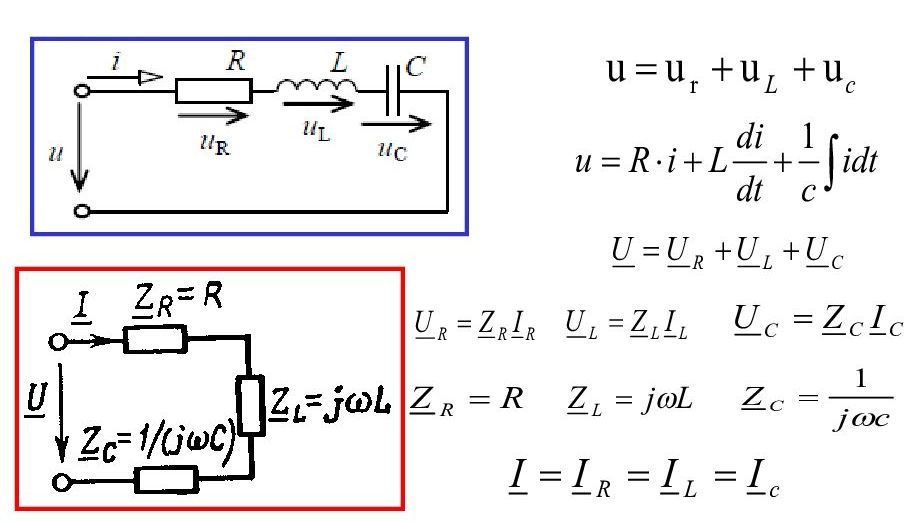
 Схема на картинке ниже содержит все элементы, которые до сих пор рассматривались отдельно в предыдущих сериях статей, а именно индуктивность, емкость и сопротивление, а также их свойства, такие как реактивное сопротивление , фаза , импеданс и т.д.
Схема на картинке ниже содержит все элементы, которые до сих пор рассматривались отдельно в предыдущих сериях статей, а именно индуктивность, емкость и сопротивление, а также их свойства, такие как реактивное сопротивление , фаза , импеданс и т.д.
| Серия статей по схемам LCR |
|
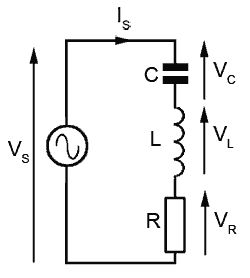
Эта серия статей учитывает влияние LC и R, соединенных последовательно и питаемых переменным напряжением. В такой схеме один и тот же ток цепи (I) протекает через все компоненты цепи, а VR , VL и VC указывает напряжения на резисторе, катушке индуктивности и конденсаторе соответственно.
В прошлой серии статей описывалось влияние внутреннего сопротивления на напряжение, измеренное на катушке индуктивности. В цепях LCR в полной цепи присутствует как внутреннее сопротивление (индуктора), так и внешнее сопротивление. Поэтому проще будет считать, что напряжение VR — это напряжение на общем сопротивлении цепи, которое складывается из внутреннего сопротивления L, добавленного к любому отдельному постоянному резистору. Там, где упоминается VS , это приложенное напряжение питания.
Соотношение фаз между напряжением питания VS и током цепи IS зависит от относительных значений индуктивности и емкости, а также от того, больше или меньше индуктивное сопротивление (XL ) емкостного сопротивления (XC). Возможны различные условия, которые можно проиллюстрировать с помощью векторных диаграмм.
На картинке ниже показаны условия цепи, когда индуктивное сопротивление (XL) больше, чем емкостное сопротивление (XC). В этом случае, поскольку и L, и C несут одинаковый ток, а XL больше, чем XC , отсюда следует, что VL должно быть больше, чем VC .
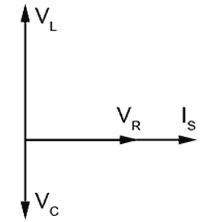
(VL = IS XL и VC = IS XC)
Помните, что VC и VL находятся в противофазе друг другу из-за их 90-градусного опережения и отставания от тока цепи (IS). Поскольку VL и VC прямо противоположны друг другу, создается результирующее напряжение, которое будет разностью между VC и VL . Это называется реактивным напряжением, и его значение можно рассчитать, просто вычитая VC из VL . Это показано на картинке ниже вектором (VL − VC).
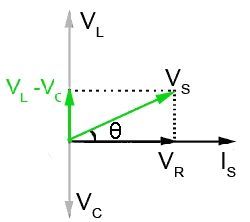
Длину вектора (VL — VC) можно получить графически, удалив часть с кончика вектора (VL), эквивалентную длине вектора (VC).
Таким образом, VS представляет собой векторную сумму реактивного напряжения (VL − VC ) и VR . Фазовый угол θ показывает, что ток цепи IS отстает от напряжения питания VS на величину от 90° до 0°, в зависимости от относительных величин (VL — VC ) и VR . Поскольку IS отстает от VS , это должно означать, что цепь в основном индуктивная, но значение индуктивности было уменьшено из-за присутствия C. Также разность фаз между IS и VS больше не составляет 90°, как это было бы, если бы цепь состояла только из индуктивности и сопротивления.
Поскольку вектора для (VL − VC), VR и VS на картинке выше образуют прямоугольный треугольник, ряд свойств и значений в цепи можно вычислить либо с помощью теоремы Пифагора, либо с помощью некоторой базовой тригонометрии.
Например:
VS2 = (VL − VC )2 + VR2
или
![]()
Полный импеданс цепи (Z) можно найти аналогичным образом:
![]()
Фазовый угол между (VL − VC ) и VR можно найти с помощью тригонометрии:
tanθ = противоположный разделить на соседний,
следовательно,
tanθ = (VL — VC ) ÷ VR
чтобы найти угол θ
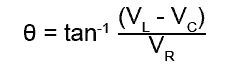
Следовательно, если (VL — VC ) и VR разделить на ток (IS ), то это позволит найти фазовый угол θ с использованием сопротивлений и реактивных сопротивлений без предварительного расчета отдельных напряжений.
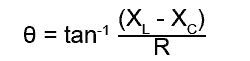
Это может быть полезно, когда необходимо выбрать номиналы компонентов для последовательной цепи, дающей требуемый угол фазового сдвига.
Картинка ниже иллюстрирует векторную диаграмму для последовательной цепи LCR, в которой XC больше XL , показывающую, что когда VC превышает VL , ситуация, показанная на картинке выше, меняется на обратную.
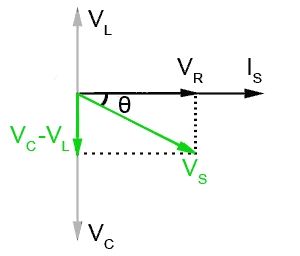
Результирующее реактивное напряжение теперь определяется как (VC — VL ), а VS представляет собой векторную сумму (VC — VL ) и VR .
Фазовый угол θ теперь показывает, что ток цепи (IS ) опережает напряжение питания (VS ) на величину от 0° до 90°. Общая схема теперь является емкостной, но в меньшей степени, чем если бы L не присутствовал.
При использовании приведенных выше формул помните, что реактивное значение (разница между VL и VC или XL и XC ) определяется путем вычитания меньшего значения из большего значения. Например, когда VC больше, чем VL:
![]()
Глядя на векторные диаграммы для цепи LCR, можно увидеть, что напряжение питания (VS ) может либо опережать, либо отставать от тока питания (IS ) в зависимости от относительных значений реактивных сопротивлений компонентов, XL и XC .
Реактивное сопротивление L и C зависит от частоты, поэтому, если частота напряжения питания VS изменяется в подходящем диапазоне, последовательная цепь LCR может действовать либо как индуктор, либо как как конденсатор, но это еще не все.
На картинке ниже показана ситуация, которая должна иметь место на определенной частоте, когда XC и XL (и, следовательно, VC и VL ) равны.
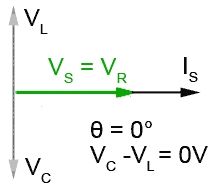
Противоположные и равные напряжения VC и VL теперь полностью компенсируют друг друга. Напряжение питания и ток в цепи теперь должны быть в фазе, поэтому цепь, по-видимому, полностью резистивная! L и C полностью «исчезли». Этот особый случай называется последовательным резонансом.
В следующей статье мы поговорим о последовательном резонансе.
С Уважением, МониторБанк