 До этой статьи мы рассматривали линейную структуру данных как статической, так и динамической природы. Теперь мы перейдем к нелинейной структуре данных. Первая структура данных в этой категории — “Деревья”.
До этой статьи мы рассматривали линейную структуру данных как статической, так и динамической природы. Теперь мы перейдем к нелинейной структуре данных. Первая структура данных в этой категории — “Деревья”.
Деревья — это нелинейные иерархические структуры данных. Дерево — это набор узлов, соединенных друг с другом с помощью “ребер”, которые либо направлены, либо неориентированы. Один из узлов обозначается как “корневой узел”, а остальные узлы называются дочерними узлами или конечными узлами корневого узла.
В общем, у каждого узла может быть сколько угодно дочерних узлов, но только один родительский узел.
Узлы дерева либо находятся на одном уровне, называемые сестринскими узлами, либо могут иметь отношения родитель-потомок. Узлы с одним и тем же родителем являются родственными узлами.
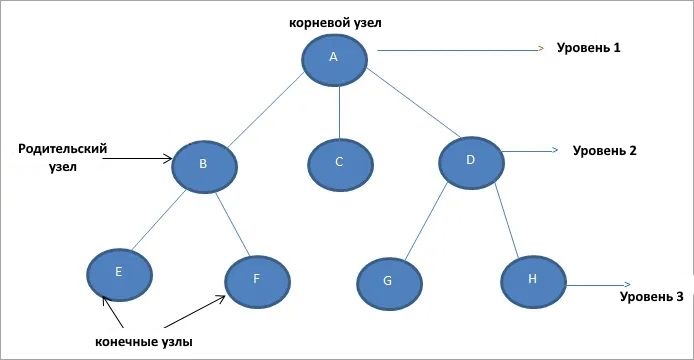
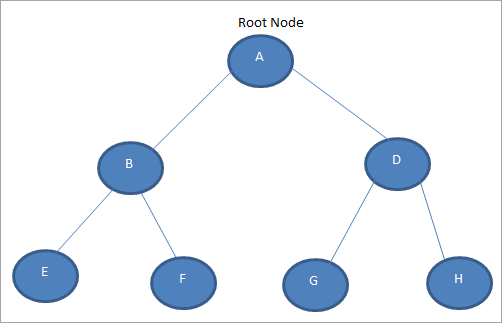
Ниже приведен пример дерева с его различными частями:
Давайте пройдемся по определениям некоторых основных терминов, которые мы используем для обозначения деревьев:
Корневой узел: это самый верхний узел в древовидной иерархии. На приведенной выше схеме узел A является корневым узлом. Обратите внимание, что корневой узел не имеет никакого родительского узла.
Конечный узел: это нижний узел в древовидной иерархии. Конечные узлы — это узлы, у которых нет дочерних узлов. Они также называются внешними узлами. Узлы E, F, G, H и C в приведенном выше дереве являются конечными узлами.
Поддерево: поддерево представляет различных потомков узла, когда корень не равен null. Дерево обычно состоит из корневого узла и одного или нескольких поддеревьев. На приведенной выше схеме (B-E, B-F) и (D-G, D-H) являются поддеревьями.
Родительский узел: любой узел, кроме корневого узла, который имеет дочерний узел.
Узел-предок: это любой узел-предшественник на пути от корня к этому узлу. Обратите внимание, что у корня нет предков. На приведенной выше схеме A и B являются предками E.
Ключ: он представляет значение узла.
Уровень: представляет поколение узла. Корневой узел всегда находится на уровне 1. Дочерние узлы корня находятся на уровне 2, внуки корня находятся на уровне 3 и так далее. В общем случае каждый узел находится на уровне выше, чем его родительский узел.
Путь: путь представляет собой последовательность последовательных ребер. На приведенной выше диаграмме путь к E равен A=>B->E.
Степень: степень узла указывает количество дочерних элементов, которые имеет узел. На приведенной выше схеме степень B и D равна 2 каждая, тогда как степень C равна 0.
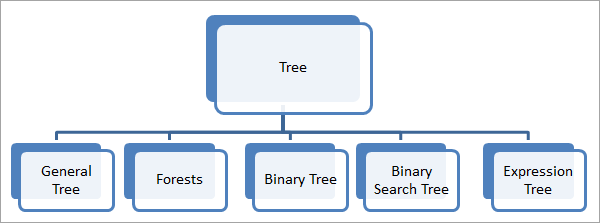
Типы деревьев C++
Древовидная структура данных может быть классифицирована на следующие подтипы, как показано на схеме ниже:
1) Общее дерево
Общее дерево — это базовое представление дерева. У него есть узел и один или несколько дочерних узлов. Узел верхнего уровня, то есть корневой узел, присутствует на уровне 1, а все остальные узлы могут присутствовать на разных уровнях.
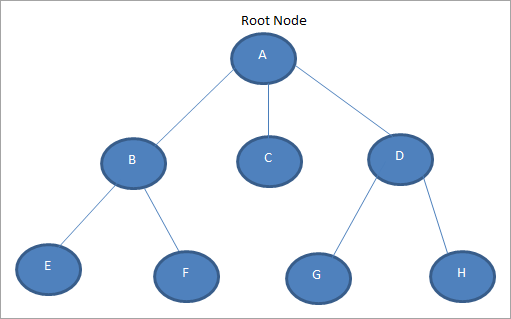
Общее дерево показано на схеме ниже:
Как показано на схеме выше, общее дерево может содержать любое количество поддеревьев. Узлы B, C и D присутствуют на уровне 2 и являются родственными узлами. Аналогично, узлы E, F, G и H также являются родственными узлами.
Узлы, присутствующие на разных уровнях, могут демонстрировать отношения родитель-потомок. На приведенной выше схеме узлы B, C и D являются дочерними элементами A. Узлы E и F являются дочерними элементами B, тогда как узлы G и H являются дочерними элементами D.
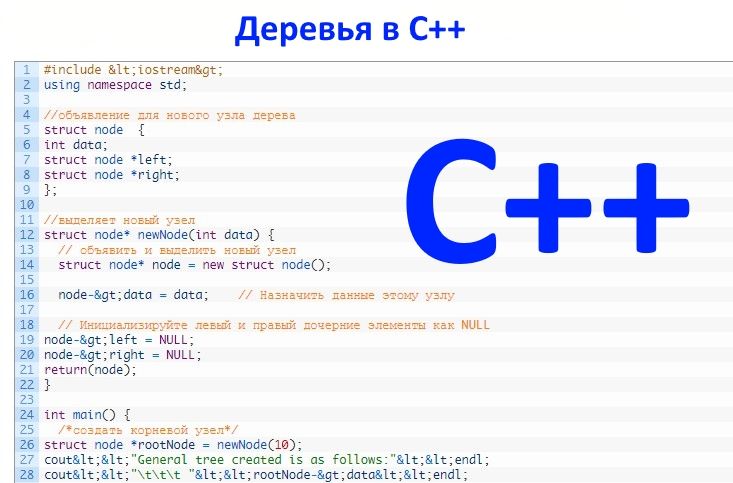
Общее дерево продемонстрировано ниже с использованием реализации C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
#include <iostream> using namespace std; //объявление для нового узла дерева struct node { int data; struct node *left; struct node *right; }; //выделяет новый узел struct node* newNode(int data) { // объявить и выделить новый узел struct node* node = new struct node(); node->data = data; // Назначить данные этому узлу // Инициализируйте левый и правый дочерние элементы как NULL node->left = NULL; node->right = NULL; return(node); } int main() { /*создать корневой узел*/ struct node *rootNode = newNode(10); cout<<"General tree created is as follows:"<<endl; cout<<"\t\t\t "<<rootNode->data<<endl; cout<<"\t\t\t "<<"/ "<<"\\"<<endl; rootNode->left = newNode(20); rootNode->right = newNode(30); cout<<"\t\t\t"<<rootNode->left->data<<" "<<rootNode->right->data; cout<<endl; rootNode->left->left = newNode(40); cout<<"\t\t\t"<<"/"<<endl; cout<<"\t\t "<<rootNode->left->left->data; return 0; } |
Вывод данных:
| Общее созданное дерево выглядит следующим образом: 10 / \ 20 30 / 40 |
2) Леса
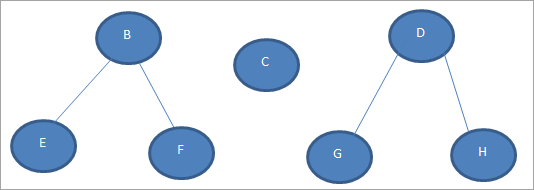
Всякий раз, когда мы удаляем корневой узел из дерева, а ребра соединяют элементы следующего уровня и корень, мы получаем непересекающиеся наборы деревьев, т.е. целый лес деревьев, как показано ниже:
На приведенной выше схеме мы получили два леса, удалив корневой узел A и три ребра, которые соединяли корневой узел с узлами B, C и D.
3) Бинарное дерево
Древовидная структура данных, в которой каждый узел имеет не более двух дочерних узлов, называется бинарным или двоичным деревом. Двоичное дерево является наиболее популярной древовидной структурой данных и используется в ряде применений, таких как вычисление выражений, базы данных и т.д.
На следующей схеме показано бинарное дерево:
На приведенной выше схеме видно, что узлы A, B и D имеют по два дочерних элемента каждый. Бинарное дерево, в котором каждый узел имеет ровно ноль или два дочерних элемента, называется полным бинарным деревом. В этом дереве нет узлов, у которых есть дочерний элемент.
Полное бинарное дерево имеет полностью заполненное двоичное дерево, за исключением самого низкого уровня, который заполняется слева направо. Бинарное дерево, показанное выше, является полным двоичным деревом.
Ниже приведена простая программа для демонстрации бинарного дерева. Обратите внимание, что результатом дерева является последовательность обхода входного дерева по порядку:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
#include<iostream> using namespace std; struct bintree_node{ bintree_node *left; bintree_node *right; int data; } ; class bst{ bintree_node *root; public: bst(){ root=NULL; } int isempty() { return(root==NULL); } void insert(int item); void displayBinTree(); void printBinTree(bintree_node *); }; void bst::insert(int item){ bintree_node *p=new bintree_node; bintree_node *parent; p->data=item; p->left=NULL; p->right=NULL; parent=NULL; if(isempty()) root=p; else{ bintree_node *ptr; ptr=root; while(ptr!=NULL){ parent=ptr; if(item>ptr->data) ptr=ptr->right; else ptr=ptr->left; } if(item<parent->data) parent->left=p; else parent->right=p; } } void bst::displayBinTree(){ printBinTree(root); } void bst::printBinTree(bintree_node *ptr){ if(ptr!=NULL){ printBinTree(ptr->left); cout<<" "<<ptr->data<<" "; printBinTree(ptr->right); } } int main(){ bst b; b.insert(20); b.insert(10); b.insert(5); b.insert(15); b.insert(40); b.insert(45); b.insert(30); cout<<"Binary tree created: "<<endl; b.displayBinTree(); } |
Вывод данных:
| Создано бинарное дерево: 5 10 15 20 30 40 45 |
4) Бинарное дерево поиска
Упорядоченное бинарное дерево называется двоичным или бинарным деревом поиска. В двоичном дереве поиска узлы слева меньше корневого узла, в то время как узлы справа больше или равны корневому узлу.
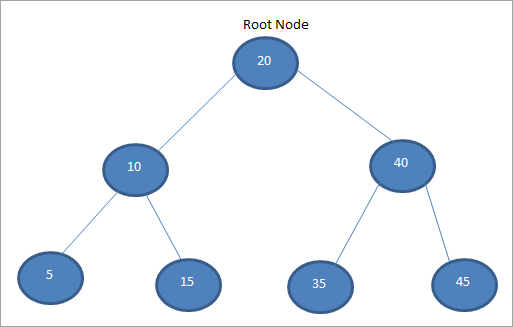
Пример бинарного дерева поиска показан ниже:
На приведенной выше схеме видно, что все левые узлы меньше 20, что является корневым элементом. С другой стороны, правые узлы больше корневого узла. Бинарное дерево поиска используется в методах поиска и сортировки.
5) Дерево выражений
Бинарное дерево, которое используется для вычисления простых арифметических выражений, называется деревом выражений.
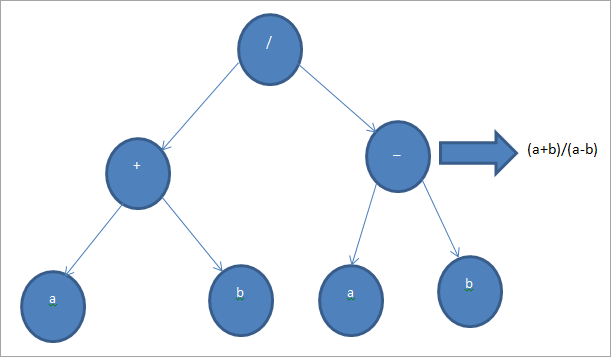
Структура простого дерева выражений показано ниже:
В приведенном выше примере дерева выражений мы представляем выражение (a + b) / (a-b). Как показано на схеме выше, нелистовые узлы дерева представляют операторы выражения, а листовые узлы представляют операнды.
Деревья выражений в основном используются для решения алгебраических выражений.
Методы обхода дерева
Линейные структуры данных, такие как массивы, связанные списки, стеки, очереди и т.д., все эти структуры данных имеют общую технику обхода, которая пересекает структуру только одним способом, т.е. линейно.
Но в случае деревьев есть разные методы обхода, перечисленные ниже:
1) По порядку: в этом методе обхода мы сначала проходим левое поддерево, пока в левом поддереве не останется больше узлов. После этого мы посещаем корневой узел, а затем переходим к обходу правого поддерева, пока в правом поддереве не останется больше узлов для обхода. Таким образом, порядок обхода по порядку — left-> root-> right .
2) Предварительный заказ: для метода обхода предварительного заказа мы сначала обрабатываем корневой узел, затем проходим все левое поддерево и, наконец, проходим правое поддерево. Следовательно, порядок обхода предварительного заказа — root-> left-> right .
3) После порядка: в технике обхода после порядка мы проходим левое поддерево, затем правое поддерево и, наконец, корневой узел. Порядок обхода для метода после порядка — это left->right->root .
Если n — корневой узел, а ‘l’ и ’r’ — левый и правый узлы дерева соответственно, то алгоритмы обхода дерева следующие:
Алгоритм по порядку (lnr):
- Пройти по левому поддереву, используя inOrder(левое поддерево).
- Перейти к корневому узлу (n).
- Пройти по правому поддереву, используя inOrder(правое поддерево).
Алгоритм предварительного заказа (nlr):
- Перейти к корневому узлу (n).
- Пройти по левому поддереву, используя предварительный заказ (левое поддерево).
- Пройти по правому поддереву, используя предварительный заказ (правое поддерево).
Алгоритм после порядка (lrn):
- Пройти по левому поддереву, используя postOrder(левое поддерево).
- Пройти по правому поддереву, используя postOrder(правое поддерево).
- Перейти к корневому узлу (n).
Из приведенных выше алгоритмов методов обхода мы можем видеть, что методы могут быть применены к данному дереву рекурсивным образом для получения желаемого результата.
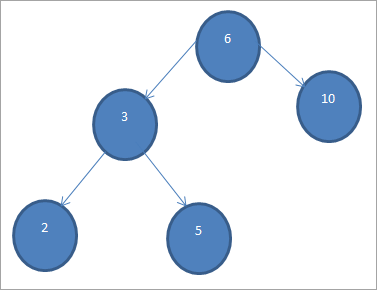
Рассмотрим следующее дерево:
Используя вышеупомянутые методы обхода, последовательность обхода для вышеупомянутого дерева приведена ниже:
Порядок обхода: 2 3 5 6 10
Предварительный обход: 6 3 2 5 10
Обход по порядку: 2 5 3 10 6
Итог
Деревья — это нелинейная иерархическая структура данных, которая применяется в области программного обеспечения.
В отличие от линейных структур данных, которые имеют только один способ обхода списка, мы можем перемещаться по деревьям различными способами.
В следующей статье мы поговорим о бинарной древовидной структуре данных в C++.
С Уважением, МониторБанк