Когда на конденсатор подается напряжение, конденсатор заряжается медленно и, наконец, достигает полностью заряженного положения. В этот момент напряжение зарядки конденсатора равно напряжению питания. Здесь конденсатор действует как источник энергии, пока подается напряжение. Конденсаторы не пропускают через них ток (i) после полной зарядки. Ток, протекающий по цепи, зависит от количества заряда на пластинах конденсаторов, а также ток прямо пропорционален скорости изменения напряжения, приложенного к схеме, т.е. i = dQ/dt = C dV (t)/dt.
Если напряжение питания переменного тока приложено к цепи конденсатора, то конденсатор непрерывно заряжается и разряжается в зависимости от частоты напряжения питания. Емкость конденсатора в цепях переменного тока зависит от частоты приложенного к нему напряжения питания. В цепях переменного тока конденсаторы пропускают ток, когда напряжение питания непрерывно изменяется во времени.
Конденсатор в цепи переменного тока
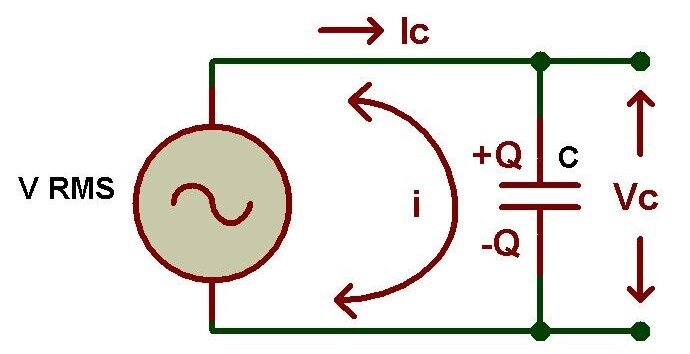
В приведенной выше схеме мы могли заметить, что конденсатор напрямую подключен к источнику переменного тока. Здесь конденсатор непрерывно заряжается и разряжается в зависимости от изменений напряжения питания, т.к. значение напряжения питания переменного тока постоянно увеличивается и уменьшается. Все мы знаем, что ток, протекающий по цепи, прямо пропорционален скорости изменения приложенного напряжения.
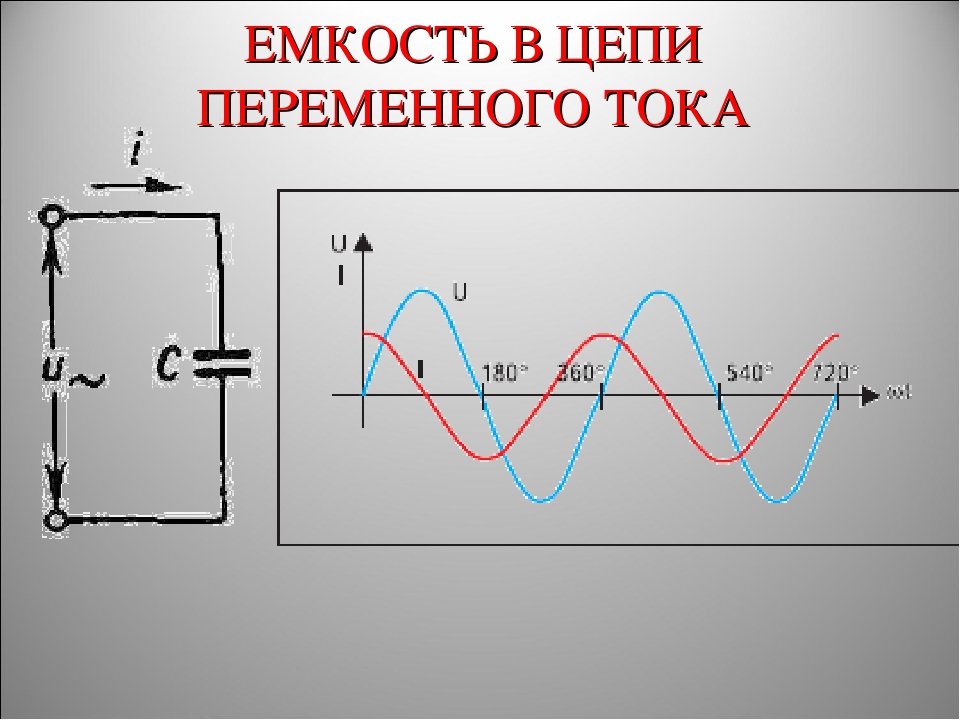
Здесь зарядный ток имеет высокое значение, если напряжение питания пересекает свое значение от положительного полупериода к отрицательному полупериоду и наоборот, т.е. при 00 и 1800 в синусоидальном сигнале. Ток через конденсатор имеет минимальное значение, когда напряжение питания синусоидальной волны пересекает свое максимальное или минимальное пиковое значение (Vm). Следовательно, мы можем сказать, что зарядный ток, протекающий по цепи, является максимальным или минимальным в зависимости от уровней напряжения питания в синусоиде.
Схема фазора в цепи переменного тока
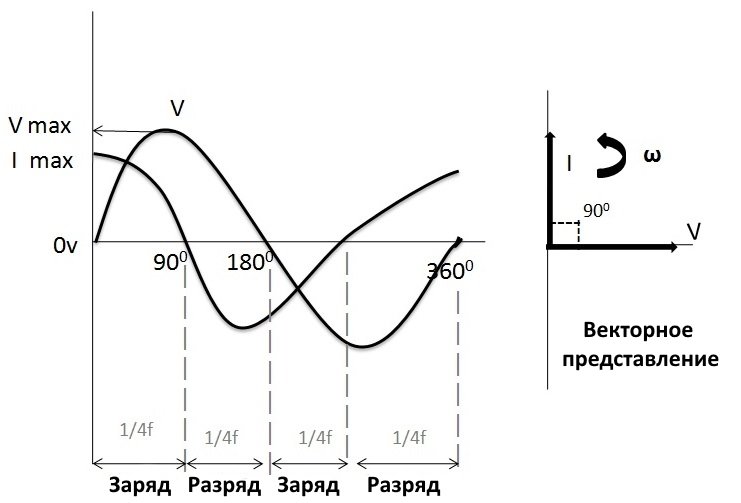
Векторная диаграмма конденсатора переменного тока показана на рисунке выше, здесь напряжение и токи представлены в синусоидальной форме. На приведенном выше рисунке мы наблюдали, что при 00 зарядный ток имеет максимальное значение, потому что напряжение медленно увеличивается в положительном направлении. При 900 ток через конденсатор не протекает, потому что в этот момент напряжение питания находится на максимальном пиковом значении.
В точке 1800 напряжение медленно уменьшается до нуля, а ток достигает максимального значения в отрицательном направлении. Зарядка снова достигает максимального значения при 3600 , потому что в этот момент напряжение питания находится на минимальном значении.
На приведенной выше картинке видно, что ток опережает напряжение на 900. Следовательно, можно сказать, что в идеальной конденсаторной схеме напряжение переменного тока отстает от тока на 900.
Емкостное реактивное сопротивление
Мы знаем, что ток, протекающий через конденсатор, прямо пропорционален скорости изменения приложенного напряжения, но конденсаторы также обладают некоторой формой сопротивления протеканию тока, как и резисторы. Это сопротивление конденсаторов в цепях переменного тока называется емкостным реактивным сопротивлением. Емкостное реактивное сопротивление — это свойство конденсатора, которое препятствует прохождению тока в цепях переменного тока. Оно обозначается символом Xc и измеряется в Ом так же, как и сопротивление.
Нам нужна дополнительная энергия по сравнению с емкостным реактивным сопротивлением, чтобы зарядить конденсатор в цепи. Это значение обратно пропорционально величине емкости и частоте напряжения питания.
Xc∝ 1/c и Xc∝ 1/f
Уравнение емкостного реактивного сопротивления и влияющие на него параметры показаны ниже.
Емкостное реактивное сопротивление,
XC = 1/2πfC = 1/ωC
XC = реактивное сопротивление конденсатора
f = частота в Гц
C = емкость конденсатора в фарадах
ω (омега) = 2πf
Из приведенного выше уравнения мы можем видеть, что емкостное реактивное сопротивление велико там, где значения частоты и емкости низкие, и на этом этапе конденсатор действует как идеальный резистор. Если частота напряжения питания высока, то значение реактивного сопротивления конденсатора низкое, а также на этом этапе конденсатор действует как хороший проводник. Из приведенного выше уравнения ясно, что реактивное сопротивление равно нулю, если частота равна бесконечности, а значение реактивного сопротивления равно бесконечности, когда частота равна нулю.
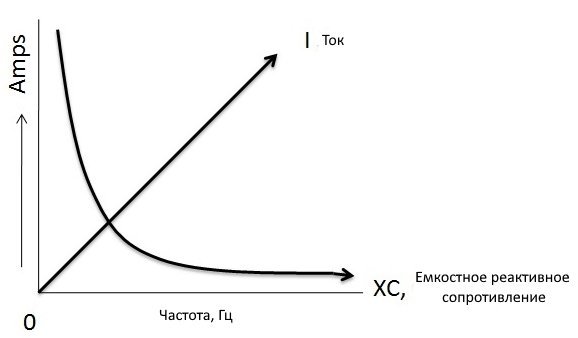
Емкостная реактивность в зависимости от частоты
На приведенной выше картинке показано соотношение между емкостным реактивным сопротивлением, током и частотой питающего напряжения. Здесь мы заметили, что если частота низкая, то реактивное сопротивление высокое. Зарядный ток увеличивается с увеличением частоты, потому что скорость изменения напряжения увеличивается со временем. Реактивное сопротивление имеет бесконечное значение, когда частота равна нулю, и наоборот.
Пример емкости переменного тока №1
Найдите среднеквадратичное значение тока, протекающего через цепь с конденсатором 3 мкФ, подключенным к источнику питания 660 В и частотой 40 Гц.
Емкостное реактивное сопротивление,
ХС = 1/2πfC
f = 40 Гц
C = 3 мкФ
Vrms = 660 В
Получается,
XC = 1/(2 × 3,14 × 40Гц × 3 × 10 -6 ) = 1326Ω
Irms = Vrms/XC = 660 В/1326 Ом = 497 мА
Пример емкости переменного тока №2
Найдите среднеквадратичное значение тока, протекающего через цепь с конденсатором 5 мкФ, подключенным к источнику питания 880 В и частотой 50 Гц.
Емкостное реактивное сопротивление,
ХС = 1/2πfC
f = 50 Гц
C = 5 мкФ
Vrms = 880 В
Получается,
XC = 1 / (2 × 3,14 × 50 Гц × 5 × 10-6) = 636 Ом
Irms = Vrms / XC = 880 В / 636 Ом = 1,38 А
Из двух приведенных выше примеров мы практически заметили, что реактивное сопротивление конденсатора зависит от частоты напряжения питания и оно обратно пропорционально. В примере №1 реактивное сопротивление составляет 1326 Ом для частоты 40 Гц, но значение реактивного сопротивления уменьшается до 636 Ом при увеличении частоты до 50 Гц, что показано в примере №2, поэтому ясно, что реактивное сопротивление конденсатора обратно пропорционально частоте.
С Уважением, МониторБанк