В схеме делителя напряжения, напряжение питания или напряжение схемы распределяется между всеми компонентами в цепи одинаково, в зависимости от емкости этих компонентов.
Сама схема емкостного делителя напряжения такая же, как и у схемы резистивного делителя напряжения. Но, как и резисторы, на схему емкостного делителя напряжения не влияют изменения частоты, даже если в ней используются реактивные элементы.
Конденсатор — это пассивный компонент, который накапливает электрическую энергию на металлических пластинах. Конденсатор состоит из двух пластин, и они разделены непроводящим или изолирующим материалом, так называемым «диэлектриком».
Здесь положительный заряд хранится на одной пластине, а отрицательный заряд — на другой пластине.
Когда на конденсатор подается постоянный ток, он полностью заряжается. Диэлектрический материал между пластинами действует как изолятор, а также препятствует прохождению тока через конденсатор.
Это сопротивление току, подаваемому через конденсатор, называется реактивным сопротивлением (XC) конденсатора. Реактивное сопротивление конденсатора также измеряется в омах.
Полностью заряженный конденсатор действует как источник энергии, т.к. конденсатор накапливает энергию и разряжает ее на компонентах схемы.
Если на конденсатор подается переменный ток, то конденсатор непрерывно заряжается и разряжает ток через свои пластины. В это время конденсатор также имеет реактивное сопротивление, которое изменяется в зависимости от частоты питания.
Мы знаем, что заряд, который хранится в конденсаторе, зависит от напряжения питания и емкости конденсатора. Таким же образом реактивное сопротивление также зависит от некоторых параметров.
Если конденсатор имеет меньшее значение емкости, то время, необходимое для зарядки конденсатора, меньше, т.е. требуется меньшая постоянная времени RC. Точно так же постоянная времени RC высока для большей емкости конденсаторов.
Получается, что конденсатор с большим значением емкости имеет меньшее значение реактивного сопротивления, тогда как меньшее значение емкости конденсатора имеет большее значение реактивного сопротивления, т.е. реактивное сопротивление конденсатора обратно пропорционально значению емкости конденсатора.
X C ∝ 1 / C
Если частота приложенного тока низкая, время зарядки конденсатора увеличивается. Это указывает на высокое значение реактивного сопротивления. Таким же образом, если частота приложенного тока высокая, то реактивное сопротивление конденсатора низкое.
Отсюда можно заметить, что реактивное сопротивление конденсатора обратно пропорционально частоте.
Наконец, мы можем сказать, что реактивное сопротивление (XC) любого конденсатора обратно пропорционально частоте (f) и значению емкости (C).
X C ∝ 1 / f
Формула емкостного реактивного сопротивления
Мы уже знаем, что емкостное реактивное сопротивление обратно пропорционально частоте и значению емкости конденсатора. Таким образом, формула реактивного сопротивления:
Х С = 1 / 2πfC
XC = реактивное сопротивление конденсатора в омах (Ом)
f = частота в герцах (Гц)
C = емкость конденсатора в фарадах (Ф)
π = числовая константа (22/7 = 3,142)
Распределение напряжения в последовательно соединенных конденсаторах
Если конденсаторы соединены последовательно, распределение напряжения рассчитывается между конденсаторами, т.к. конденсаторы имеют разные значения напряжения в зависимости от значений емкости при последовательном соединении.
Реактивное сопротивление конденсатора, препятствующего прохождению тока, зависит от значения емкости и частоты приложенного тока.
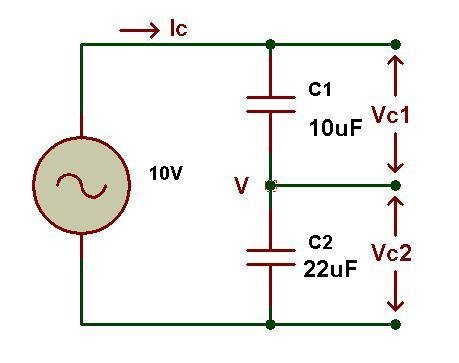
Итак, теперь давайте посмотрим, как реактивное сопротивление влияет на конденсаторы, вычислив значения частоты и емкости. На картинке ниже показана схема емкостного делителя напряжения, в которой последовательно соединены 2 конденсатора.
Емкостной делитель напряжения
Два последовательно соединенных конденсатора, имеют значения емкости 10 мкФ и 22 мкФ соответственно. В схеме, напряжение в цепи равно 10В, это напряжение распределяется между обоими конденсаторами.
При последовательном соединении все конденсаторы имеют одинаковый заряд (Q), но напряжение питания (VS) не одинаково для всех конденсаторов.
Напряжение цепи распределяется между конденсаторами в зависимости от значений емкости конденсаторов, т.е. в соотношении V = Q/C.
По этим значениям мы должны рассчитать реактивное сопротивление (XC) каждого конденсатора, используя значения частоты и емкости конденсаторов.
Пример емкостного делителя напряжения №1
Теперь мы рассчитаем распределение напряжения на конденсаторы 10 мкФ и 22 мкФ, которые показаны на картинке выше, которые имеют напряжение питания 10 В с частотой 40 Гц.
Реактивное сопротивление конденсатора 10 мкФ,
X C1 = 1 / 2πfC1 = 1 / (2 * 3,142 * 40 * 10 * 10-6) = 400 Ом
Реактивное сопротивление конденсатора 22 мкФ,
X C\2 = 1 / 2πfC2 = 1 / (2 * 3,142 * 40 * 22 * 10-6) = 180 Ом
Общее емкостное реактивное сопротивление цепи составляет,
XC = X C1 + X C2 = 400 Ом + 180 Ом = 580 Ом
CT = C1C2 / (C1 + C2) = (10 * 22 * 10-12) / (32 * 10-6) = 6,88 мкФ
XCT = 1 / 2πfC T = 1 / (2 * 3,142 * 40 * 6,88 * 10-6) = 580 Ом
Ток в цепи равен,
I = V/X C = 10 В/580 Ом = 17,2 мА
Теперь падение напряжения на каждом конденсаторе составляет
V C1 = I * X C1 = 17,2 мА * 400 Ом = 6,9 В
V C2 = I * X C2 = 17,2 мА * 180 Ом = 3,1 В
Пример емкостного делителя напряжения №2
Теперь мы рассчитаем падение напряжения на конденсаторах 10 мкФ и 22 мкФ, которые подключены последовательно и работают с напряжением питания 10 В с частотой 4000 Гц (4 КГц).
Реактивное сопротивление конденсатора 10 мкФ,
X C1 = 1/2πfC1 = 1 / (2 * 3,142 * 4000 * 10 * 10-6) = 4 Ом
Реактивное сопротивление конденсатора 22 мкФ,
XC\2 = 1/2πfC2 = 1 / (2 * 3,142 * 4000 * 22 * 10-6) = 1,8 Ом
Общее емкостное реактивное сопротивление цепи составляет,
XC = XC1 + XC2 = 4 Ом + 1,8 Ом = 5,8 Ом
CT = C1C2/(C1 + C2) = (10 * 22 * 10-12) / (32 * 10-6) = 6,88 мкФ
XCT = 1/2πfC T = 1 / (2 * 3,142 * 4000 * 6,88 * 10-6) = 5,8 Ом
Ток в цепи равен,
I = V/XCT = 10 В / 5,8 Ом = 1,72 А
Теперь падение напряжения на каждом конденсаторе составляет
VC1 = I * X C1 = 1,72 A * 4 Ом = 6,9 В
VC2 = I * X C2 = 1,72 A * 1,8 Ом = 3,1 В
Из двух приведенных выше примеров мы можем сделать вывод, что конденсатор с более низким значением (10 мкФ) будет заряжаться до более высокого напряжения (6,9 В), а конденсатор с более высоким значением (22 мкФ) будет заряжаться до более низкого уровня напряжения (3,1 В).
Наконец, сумма двух значений падения напряжения на конденсаторах равна напряжению питания (т.е. 6,9 В + 3,1 В = 10 В). Эти значения напряжения одинаковы для всех значений частоты, поскольку падение напряжения не зависит от частоты.
Падение напряжения на двух конденсаторах одинаково в обоих примерах, где частота различается. Частота составляет 40 Гц или 40 кГц, падение напряжения на конденсаторах одинаково в обоих случаях.
Ток, протекающий по цепи, изменяется в зависимости от частоты. Ток будет увеличиваться с увеличением частоты, он составляет 17,2 мА для частоты 40 Гц, но 1,72 А для частоты 4KHZ, то есть ток увеличится почти в 100 раз при увеличении частоты с 4 Гц до 4 Гц.
Наконец, мы можем сказать, что ток, протекающий по цепи, прямо пропорционален частоте (I α f).
Итог
Противодействие протеканию тока в конденсаторе, называется реактивным сопротивлением (XC) конденсатора. На это емкостное реактивное сопротивление влияют такие параметры, как значение емкости, частота напряжения питания, а также эти значения обратно пропорциональны реактивному сопротивлению. Схема делителя переменного напряжения распределяет напряжение питания на все конденсаторы в зависимости от их емкости. Эти падения напряжения на конденсаторах одинаковы для любой частоты напряжения питания. т.е. падение напряжения на конденсаторах не зависит от частоты. Но текущий ток зависит от частоты, а также эти два значения прямо пропорциональны друг другу. Но в схемах делителя напряжения постоянного тока вычислить падение напряжения на конденсаторах — непростая задача, поскольку оно зависит от значения реактивного сопротивления, поскольку конденсаторы блокируют прохождение постоянного тока через него после полной зарядки.
Цепи емкостного делителя напряжения используются в крупных электронных устройствах. В основном они используются в емкостных чувствительных экранах, которые изменяют свое выходное напряжение при прикосновении пальца человека. А также используются в трансформаторах для увеличения падения напряжения, где обычно сетевой трансформатор содержит микросхемы и компоненты с низким падением напряжения. Наконец, нужно сказать, что в схеме делителя напряжения падение напряжения на конденсаторах одинаково для всех значений частоты.
С Уважением, МониторБанк