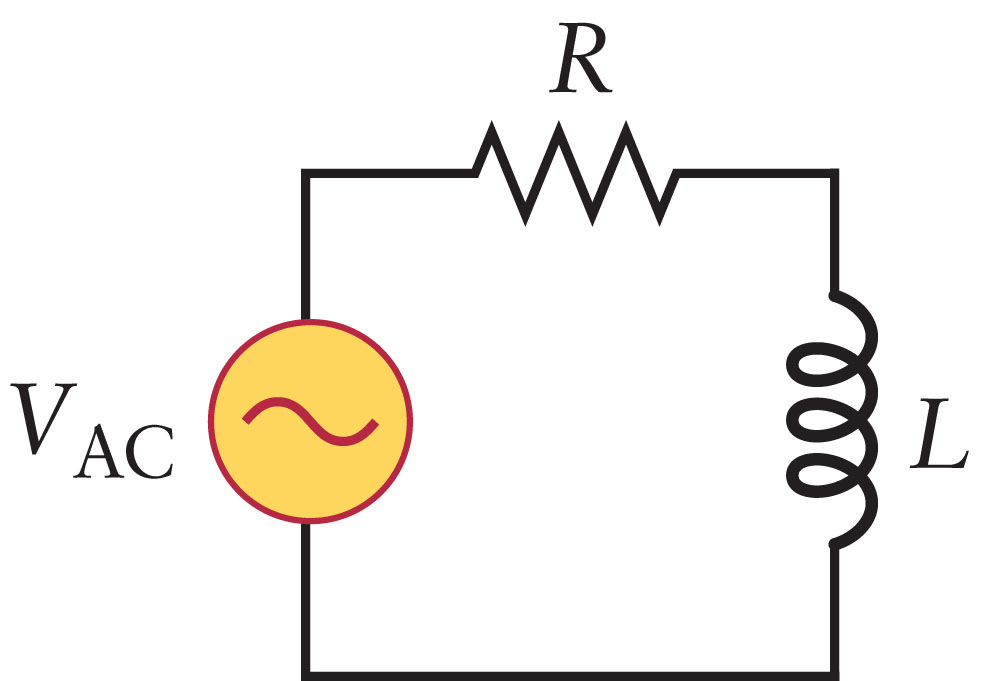
 Есть несколько способов использования векторных диаграмм для получения важных данных о цепях LCR. Например: «Какое напряжение питания потребуется для обеспечения определенного напряжения на катушке индуктивности в цепи?» или «Какова будет разность фаз между напряжением питания и током питания при определенной рабочей частоте?» и многие другие.
Есть несколько способов использования векторных диаграмм для получения важных данных о цепях LCR. Например: «Какое напряжение питания потребуется для обеспечения определенного напряжения на катушке индуктивности в цепи?» или «Какова будет разность фаз между напряжением питания и током питания при определенной рабочей частоте?» и многие другие.
| Серия статей по фазам и фазорам |
|
На картинках ниже представлены три различных метода использования векторных диаграмм для нахождения некоторой неизвестной величины.
Изучите эти три метода, и, ознакомившись с ними, вы сможете выбрать лучший из них для решения любой конкретной задачи, связанной со значениями и фазовыми углами токов и напряжений переменного тока в цепи LCR.
Способ 1. Расчет по масштабному чертежу
Поскольку компоненты схемы соединены последовательно, IS является общим для всех компонентов, поэтому IS будет эталонным вектором. Он нарисован под углом 0° (по горизонтали справа от исходной точки). Поскольку задача требует только напряжения, масштаб IS не имеет значения.
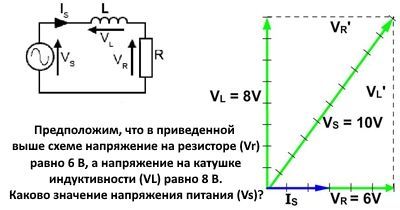
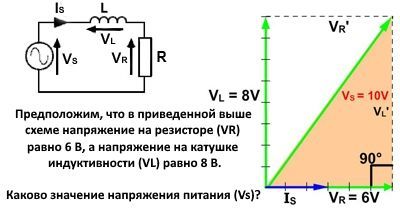
Нарисован вектор длиной 6 единиц (см, дюйм и т.д.). Поскольку и ток резистора, и напряжение всегда находятся в фазе друг с другом, VR находится в фазе с эталонным вектором IS . Значение отображается как VR = 6V. (Маленькие деления на векторе даны здесь только для того, чтобы показать масштаб.)
В чистом индукторе напряжение (VS) опережает ток (IS) на 90°, поэтому вектор на 8 В отсчитывается вертикально от общей точки начала координат.
Линия такой же длины, как и параллельная VR , проведена из вершины VL , чтобы сформировать вершину прямоугольника (VR‘).
Правая сторона прямоугольника (VL‘) проводится от вершины (VR‘) на ту же длину, что и параллельная (VL).
Вектор, показывающий VS , теперь можно провести от исходной точки по диагонали к противоположному углу прямоугольника.
Измеренная длина этого вектора будет равна сумме векторов VR и VL , что в данном случае будет равно 10 В.
Метод 2. Вычисление по теореме Пифагора
Поскольку в этом примере площадь внутри VS , VL и VR представляет собой прямоугольный треугольник, длину гипотенузы (VS) можно найти с помощью теоремы Пифагора, которая гласит:
Квадрат гипотенузы (VS в этом примере) прямоугольного треугольника равен сумме квадратов двух смежных сторон (VL‘ и VR ).
Формула:
1. VS 2 = VL 2 + VR 2 (используя обозначения векторной диаграммы на картинке выше).
2. VS 2 = 8 2 + 6 2 (обозначения заменить известными значениями).
3. VS 2 = 64 + 36 = 100 (рассчитать значение VS 2 ).
4. ВС 2 =100 (найдите квадратный корень из VS 2 , чтобы получить VS )
5. Ответ: VS = 10 В (помните, в каких единицах вы работаете — в нашем примере вольты).
Метод 3. Использование обратных тригонометрических функций
Формула нахождения угла зависит от того, какие стороны треугольника имеют известное значение. Выбор для нахождения неизвестного угла Θ (в градусах) между:
Метод а: Θ° = sin -1 (Противоположный/гипотенуза)
Метод b: Θ° = cos -1 (Смежный / гипотенуза)
Метод c: Θ° = tan -1 (Противоположный/Смежный)
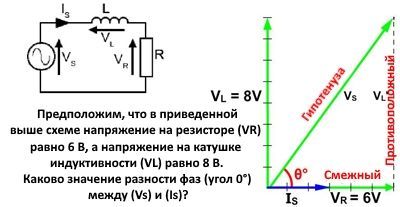
Даже когда значение гипотенузы (VS ) неизвестно (как на картинке выше), можно использовать формулу tan -1 (метод с) для нахождения угла Θ:
Θ° = tan-1 (напротив / рядом)
Θ° = tan-1 (8/6)
Θ° = tan-1 1,333333333
Θ = 53,13 °
Для закрепления изученного материала пройдите наш тест.
С Уважением, МониторБанк