 При обсуждении фазовых сдвигов между токами и напряжениями в цепях переменного тока можно использовать диаграммы, показывающие множественные формы сигналов, как в предыдущей статье, но это требует большого количества сложных диаграмм сигналов, которые во многих случаях трудно интерпретировать.
При обсуждении фазовых сдвигов между токами и напряжениями в цепях переменного тока можно использовать диаграммы, показывающие множественные формы сигналов, как в предыдущей статье, но это требует большого количества сложных диаграмм сигналов, которые во многих случаях трудно интерпретировать.
| Серия статей по фазам и фазорам |
Если бы потребовались расчеты с использованием этих форм сигналов, формы сигналов также должны были бы быть точно отрисованы в масштабе.
Гораздо более удобным методом является замена диаграмм синусоиды векторными диаграммами. Использование нескольких фактов о синусоидальной волне обеспечивает гораздо более простой способ представления волны.
Синусоидальная волна имеет только одну частоту, поэтому ее можно представить, просто выбрав подходящую точку на горизонтальной линии, которая представляет подходящий диапазон частот.
Синусоидальная волна будет иметь определенную амплитуду, это можно представить с помощью вертикальной линии, равной амплитуде волны.
Таким образом, сложный рисунок синусоидальной формы можно упростить до пары прямых линий; один представляет частоту, а другой показывает амплитуду. Проблема здесь, однако, состоит в том, чтобы нарисовать диаграмму, которая может представлять ряд синусоидальных волн, каждая из которых имеет одинаковую частоту, но с разными фазовыми соотношениями друг к другу, и именно здесь используются вектора.
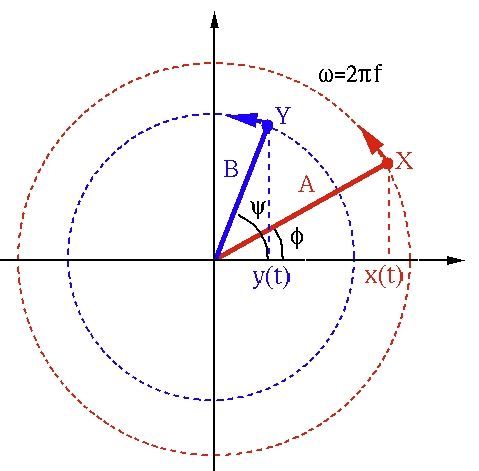
Вектор представляет собой прямую линию, нарисованную таким образом, что ее длина связана с амплитудой представленной синусоиды, а ее угловое положение относительно других векторов связано с разностью фаз между величинами.
Связь между вектором и одиночной синусоидой показана на видео ниже. Вектор, представленный стрелкой, вращается против часовой стрелки вокруг центральной исходной точки, описывая синусоиду по мере ее вращения.
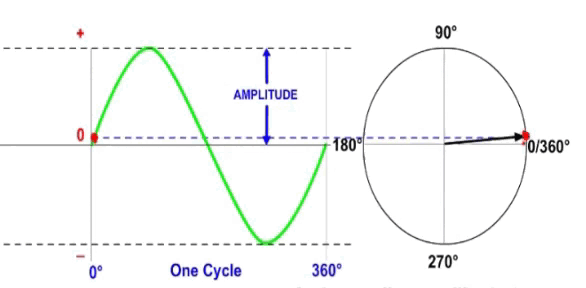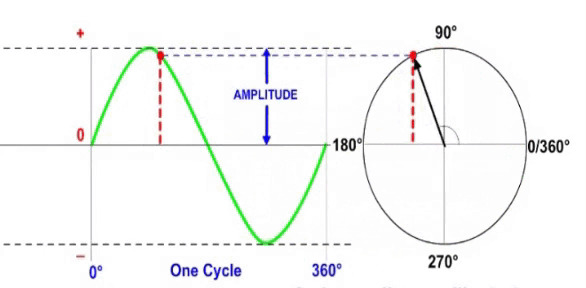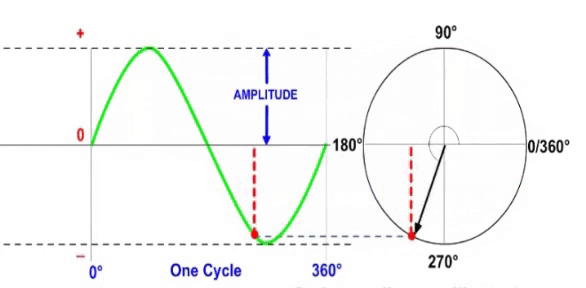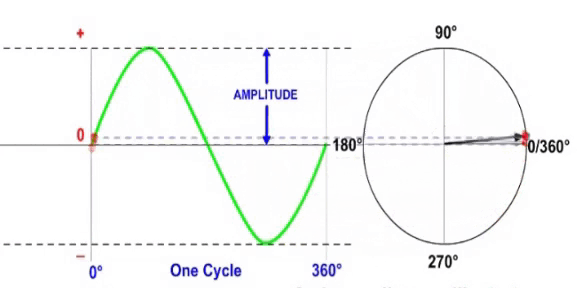
Обратите внимание, что:
- В любой момент времени длина красной пунктирной линии представляет собой мгновенное значение волны.
- Длина вектора представляет собой амплитуду волны.
- Угол вектора определяет фазу сигнала.
Приращения угла вектора на круговой диаграмме эквивалентны приращениям времени или угла вдоль горизонтальной оси диаграммы формы волны. Таким образом, с добавлением угловой информации вектор дает относительно простой способ показать сложные взаимосвязи, существующие между синусоидами в цепи переменного тока.
Угловая скорость
Поскольку вектор вращается, скорость, с которой он вращается вокруг исходной точки, будет зависеть от частоты (ƒ) представляемой волны. За одну секунду вектор повернется на ƒ оборотов или на ƒ x 360° (поскольку один оборот = 360°).
В расчетах, связанных с таким вращением, чаще используется угловая единица радиан (рад), где 360 ° = 2π рад. Таким образом, можно сказать, что вектор вращается на 2πƒ радиан в секунду. Это называется угловой скоростью вектора и обычно обозначается 2πƒ или, альтернативно, символом ω (омега).
В следующей статье мы поговорим о векторных диаграммах.
С Уважением, МониторБанк