 Индуктивные элементы, то есть катушки и дроссели, используются в схемах, а их свойства зависят от частоты тока. Обычно их делают в виде катушки с определенным количеством витков медной проволоки, намотанных на магнитопроводе. Вообще, производится множество различных типов элементов с индуктивностью.
Индуктивные элементы, то есть катушки и дроссели, используются в схемах, а их свойства зависят от частоты тока. Обычно их делают в виде катушки с определенным количеством витков медной проволоки, намотанных на магнитопроводе. Вообще, производится множество различных типов элементов с индуктивностью.
Индуктивность — это свойство катушки, которое противодействует любому изменению тока, протекающего через нее. Этот механизм является результатом действия индукции электродвижущей силы (ЭДС) в катушке. Катушка с индуктивностью 1 Гн дает ЭДС 1 В, если протекающий ток изменяется со скоростью 1 А/с (1 Гн = 1 В с/А).
Настроенные фильтры (резонансные контуры)
Они используются для выбора или ослабления определенных частот. Для этого вам нужны катушки с высоким значением добротности и хорошей стабильностью. Такие катушки обычно мотаются без сердечника или имеют сердечник из карбонила или феррита — часто с воздушным зазором. Также популярны тороидальные катушки, катушки с регулируемой индуктивностью, экранированные или неэкранированные.
Фильтры радиопомех (защита от помех)
Они используются для подавления нежелательных радиочастотных сигналов. Такая катушка должна иметь высокий импеданс в большом диапазоне частот, здесь подойдут катушки с ферритовыми сердечниками. При малых токах часто используются тороидальные сердечники, которые имеют замкнутую магнитную цепь и низкое поле рассеивания. При более высоких токах вводится зазор или используется сердечник с разомкнутой магнитной цепью, например ферритовый стержень.
Фильтрация постоянного тока и накопление энергии
В импульсных источниках питания дроссели используются для фильтрации высокочастотных помех, а в DC/DC преобразователях — для накопления энергии. В таких случаях важно, чтобы катушка хорошо работала с высокой составляющей постоянного тока без насыщения сердечника. В этом случае, чаще всего, используются ферритовые сердечники.
Катушки показывают частотно-зависимое сопротивление, которое называется реактивным сопротивлением, и сопротивление постоянному току, которое фактически является сопротивлением используемого провода. Индуктивное реактивное сопротивление XL рассчитывается по формуле:
![]()
где f — частота
![]() Импеданс Z катушки на заданной частоте представляет собой комплексное значение сопротивления и реактивного сопротивления.
Импеданс Z катушки на заданной частоте представляет собой комплексное значение сопротивления и реактивного сопротивления.
![]()
Чтобы было легче понять катушку как элемент электрической схемы, мы можем использовать упрощенную эквивалентную схему:
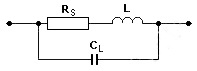
где:
L — индуктивность,
RS — последовательное сопротивление (сопротивление провода + другие потери в проводе и сердечнике),
CL — внутренняя емкость катушки, например, емкость между слоями обмотки, также известная как емкость утечки, паразитная или диффузная емкость.
Качество Q — это отношение реактивного сопротивления катушки к последовательному сопротивлению. Более низкое сопротивление дает более высокую добротность, и тогда фильтры имеют больший наклон.
Q = X L / R S
Собственная емкость катушки CL вместе с индуктивностью образует резонансный контур. Частота такого контура называется частотой собственного резонанса SRF. Собственная емкость может быть проблематичной на более высоких частотах, если она не учтена в расчетах. Частота измерения добротности должна быть не более 1/10 от этой частоты.
Расчет катушки без сердечника
Нас может заинтересовать энергия, запасенная в катушке. Ее можно рассчитать по формуле:
W = 1/2 x L x I2
где: W — энергия в Дж, L — индуктивность катушки, I — ток, протекающий через катушку.
Прежде чем приступить к расчету катушки, следует сказать, что прямой участок кабеля тоже имеет индуктивность. Это следует особенно отметить при работе с высокими частотами. Поэтому выводы элементов должны быть как можно короче, например, при последовательном соединении с конденсатором. В противном случае может возникнуть колебательный контур.
Формула индуктивности проводника следующая:
![]()
Учитывая длину проводника l и диаметр d в см, индуктивность выражается в мкГн (микрогенри). Фактор x зависит от частоты и формы. Прямой провод и высокий дают x = 1, низкая частота x = 0,75. Если провод гнуть, индуктивность будет меньше. Однооборотный круг имеет x = 2,45 на высоких частотах и 2,20 на низких частотах, а квадрат имеет 2,85 и 2,60 соответственно.
Если индуктивность должна быть увеличена, магнитный материал, например, феррит, может быть обмотан проводником, или несколько катушек могут быть обмотаны по спирали. В последнем случае взаимодействие витков будет большим (взаимная индуктивность витков). Индуктивность катушки увеличивается пропорционально квадрату числа витков в катушке.
Индуктивность однослойной воздушной катушки можно рассчитать по формуле:
![]()
где: длина катушки l и диаметр d в см, n — количество витков, L — индуктивность катушки в мГн (миллигенрах). Наибольшее значение Q будет получено, когда длина катушки в 2–2,5 раза больше ее диаметра, диаметр катушки должен быть в 5 раз больше диаметра провода.
Индуктивность многослойной воздушной катушки рассчитывается по формуле:
![]()
где: d — среднее значение диаметра, a — толщина намотки по радиусу (все в см). L — индуктивность в мкГн (микрогенри).
Для печатных катушек, которые изготовлены на ламинированных печатных платах с толщиной пленки 35 мкм (микрометров), индуктивность рассчитывается по следующей формуле:
L = nD m (nK 1 + K 2 )
где:
L — индуктивность в мкГн (microHenrach)
n — количество витков
Dm = c + d — диаметр катушки в см, (см. рисунок ниже) Константа
K1 , считывается из диаграммы:
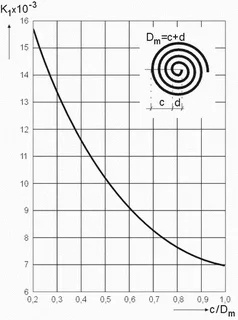
Константа K1 , считайте из диаграммы:
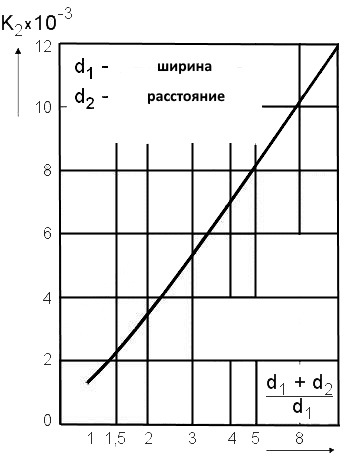
В случае конструкции катушки, отличной от круглой со спиральной намоткой, для расчета расчетного диаметра Dm можно использовать приблизительные формулы преобразования:
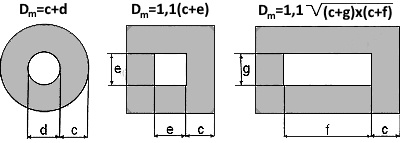
Пример: печатная катушка с d 1 = d 2 = 0,5 мм, толщиной слоя меди 35 мкм (микрометр), 14 витков и d = 10 мм.
Расчет индуктивности:
Для c = n (d 1 + d 2)= 14 мм вы получите Dm = 14 + 10 = 24 мм.
Для c / Dm = 14/24 = 0,58 вы получите K 1 = 9,2 × 10 — 3
Для ( d 1 + d 2 ) / d 1 = 2 получаем K 2 = 3,5 × 10 -3
Из чего вычисляем окончательный результат:
L= 14 x 2,4 (14 x 9,2 x 10 -3 + 3,5 x 10 -3 ) = 4,45 мкГн (микрогенра).
Катушки с сердечником
Для увеличения индуктивности, как упоминалось ранее, можно использовать сердечник из ферромагнитного материала. Наиболее распространенные материалы — ферриты, железный порошок (карбонильное железо). Их определяют как магнитомягкие материалы, т.е. когда электромагнитное поле престает работать, большая часть их магнитного потока исчезает. Противоположными являются твердые магнитные материалы, то есть те, которые используются, например, с постоянными магнитами.
Феррит — это керамический микрокристаллический материал, состоящий из крошечных кристаллов оксида железа (Fe2O3) и металлических примесей. Наиболее распространены комбинации марганец-цинк (MnZn) и никель-цинк (NiZn).
Марганцево-цинковые ферриты имеют самую высокую диэлектрическую проницаемость (ui) и индукцию насыщения потока (BS), тогда как никель-цинковые ферриты имеют более высокое сопротивление (меньшие потери) и лучше всего подходят для частот выше 1 МГц.
Достоинствами ферритов являются: очень высокая проницаемость (u и 100-10000), низкие потери и возможность работы на высоких частотах, недостаток — малая индукция насыщения (BS <0,5T). Это означает, что ферриты очень легко насыщаются, и это необходимо учитывать при работе со значительными компонентами тока. Чтобы противодействовать этому, используйте ферритовые сердечники с разомкнутой магнитной цепью, например, в форме стержня, или введите воздушный зазор в магнитную цепь.
Ферритовые сердечники используются для высокочастотных катушек, фильтров подавления помех (RFI) и трансформаторов питания, работающих на частоте до 1 МГц. Они выпускаются в виде тороидов, чашечных сердечников, сердечников с фитингами RM, C и E, буртиков, резьбовых стержней, блоков и т.д.
Порошковые ядра — как следует из названия — состоят из порошкового железа, в котором частицы изолированы друг от друга, например, путем окисления поверхности. После добавления связующего материал прессуется для придания формы и нагреваются в печи.
Самым большим преимуществом порошковых сердечников по сравнению с ферритами является то, что они выдерживают высокие токи, протекающие в обмотке, индукция насыщения (BS) составляет около 1,5 Тл. Они также термостабильны и обладают высоким качеством, а также могут выдерживать высокие частоты. Их серьезный недостаток — низкая проницаемость (ui = 2 — 90). Это связано с наличием большого количества небольших воздушных зазоров между частицами железа, что делает общий зазор очень большим.
Порошковые сердечники используются в основном для фильтрации постоянного и переменного тока низкой частоты (50 Гц). Они также используются в качестве дросселей для накопления энергии в импульсных стабилизаторах, фильтрах и для согласования импеданса на высоких частотах. Эти сердечники в основном изготавливаются тороидальными.
Сердечники из листовой стали используются почти исключительно для производства сетевых трансформаторов, где потери (вызванные наведенными вихревыми токами) настолько велики, что их практически невозможно использовать для частот выше 1 кГц.
При разработке катушек с ферромагнитными сердечниками необходимы некоторые знания в области магнетизма. Итак, начнем с основ теории магнетизма.
Магнитное поле
Когда ток проходит через катушку, намотанную вокруг сердечника, создается магнитодвижущая сила (ммс), которая создает магнитный поток в сердечнике. Величина этого потока зависит от сопротивления сердечника (Rm). Сопротивление можно приравнять к «магнитному сопротивлению» (аналог закона Ома U = I x R).
![]()
Единицей измерения магнитоэлектрической силы является сила тока, но она выражается в А, поскольку катушка безразмерна. Единица магнитного потока — 1 Вебер (Вб).
Если магнитодвижущая сила связана с эффективным значением длины магнитной линии (l e) в метрах, то сила магнитного поля получается в А/м.
H = N x I / l e
Таким образом, сила магнитного поля равна количеству витков и силы тока, деленного на эффективное значение длины пути потока. Обратите внимание, что действующее значение не равно физической длине сердечника.
Плотность потока B — также известная как индукция — это поток, деленный на эффективную магнитную площадь.
![]()
Плотность потока B выражается в единицах Тесла (Тл). 1T = 1 Вт/м 2 .
Кривая гистерезиса
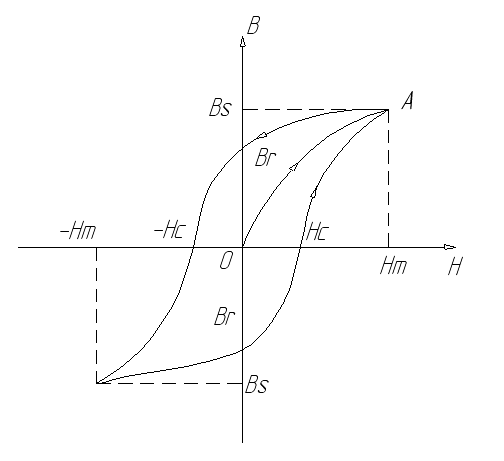
Петля B/H показывает зависимость плотности потока материала B от напряженности магнитного поля H. В ферромагнитном материале в состоянии покоя магнитные домены неупорядочены, беспорядочно расположены в разных направлениях. В целом их магнитные действия компенсируют друг друга. Когда вводится внешнее магнитное поле, молекулярные магнитные домены становятся идентичными магнитному потоку. Таким образом, чем выше напряженность магнитного поля H, тем больше магнитных доменов возвращается. Когда все частицы, то есть магнитные домены, будут направлены в одном направлении, материал станет насыщенным BS и никакая большая индукция (плотность потока) не может быть достигнута, даже если напряженность магнитного поля H дополнительно увеличивается. Когда мы уменьшаем напряженность магнитного поля, кривая намагничивания не возвращается к предыдущему пути, потому что некоторые из магнитных доменов не вернуться в прежнее положение. Когда напряженность магнитного поля равна нулю (H = 0), в материале все еще есть некоторый поток. Эта плотность потока называется остаточной магнитной индукцией Br . Чтобы очистить поток сердечника, требуется поток в противоположном направлении. Необходимая для этого интенсивность магнитного потока называется коэрцитивной силой Hc .
Магнитная проницаемость
Формула для связи между индукцией B и напряженностью магнитного поля H приведена ниже:
![]()
Где u — магнитная проницаемость, которую можно сравнить с «магнитной проводимостью». В графическом представлении проницаемость — это наклон кривой гистерезиса. Проницаемость является широким определением и по существу равна u0 xur , где u0 — проницаемость вакуума, а aur — относительная диэлектрическая проницаемость по отношению к u0 . Например, ur = 100 означает, что проницаемость материала в 100 раз больше проницаемости вакуума. Эта формула также может быть записана как:
![]()
Проницаемость вакуума равна:
![]()
В замкнутой магнитной цепи, такой как тороид, ur называется начальной проницаемостью (или диэлектрической проницаемостью тороида на тории). Он имеет правильное значение только при низкой плотности потока (B <0,1 мТл).
В магнитной цепи с воздушным зазором u r называется эффективной проницаемостью ue . В связи с тем, что проницаемость материала не является линейной как функция Bi H (кривая гистерезиса), упоминаются также другие типы проницаемости.
Амплитудная магнитная проницаемость (ua) , т.е. проницаемость, определяемая, когда ток через катушку является чисто переменным током. Уже при нескольких mT может быть большое отклонение по сравнению с ur . Она максимальна около половины индукции насыщения Bs , где она может быть в 2-3 раза больше. Проницаемость зависит от напряженности поля.
Обратная проницаемость (инкрементная) возникает, когда есть постоянная и переменная составляющие тока — например, в катушке фильтра источника питания. В этом случае проницаемость изменяется в зависимости от напряженности магнитного поля. Железный сердечник приводит к увеличению проницаемости до 10 000 А/м, в то время как ферриты уже при нескольких сотнях А/м насыщаются и теряют проницаемость.
Расчет катушки с сердечником
Для простого расчета сердечника технические данные дают эффективные магнитные размеры , которые определяются как: эффективная длина le , эффективная площадь Ae , эффективный объем Ve . Если сердечник не тороидальный, размеры даны для тороида с аналогичными свойствами. Сумма Ie/Ae называется коэффициентом сердечника (фактором формы).
Для расчета индуктивности используется следующая формула:
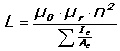
Чтобы упростить расчет, часто берутся проницаемость и коэффициент керна, а также дается коэффициент AL.
![]()
так:
L = n 2 x AL
Пример: вам нужна катушка 100 мкГн , сердечник AL = 800 нГн/н 2 . Решение:
![]()
Не забудьте указать L в nH, при условии, что AL задано в nH/n 2.
Ферритовые стержни используются не только в качестве сердечников антенны, но также часто в качестве сердечников в радиочастотных катушках, а также в катушках помехозащитных фильтров. У них разомкнутая магнитная цепь, а это значит, что через катушки могут протекать большие токи, не вызывая насыщения сердечника.
Индукция (плотность потока) в сердечнике
Важно рассчитать значение индукции B в сердечнике, чтобы избежать насыщения. Если сердечник насыщен, он имеет проницаемость 1, а индуктивность катушки такая же, как если бы это была воздушная катушка. Кроме того, возникают большие потери, которые преобразуются в тепло, особенно на высоких частотах. Индукцию можно рассчитать несколькими способами. Один из них — сначала рассчитать напряженность поля H по формуле:
H = n x I / Ie
а затем рассчитайте индукцию по формуле:
![]()
Индукция B получается в Тесла. Если это чистый постоянный ток, можно использовать следующую формулу:
![]()
где: L — индуктивность, I — ток, n — количество витков, Ae — эффективная поверхность. Для нефильтрованного двухполовинного выпрямленного тока применяется следующая формула:
![]()
где: Uэфф — действующее значение пульсирующего напряжения, f — частота. Мы часто имеем дело с напряжением с определенной пульсацией. Затем можно точно рассчитать индукцию, или, если принято слегка завышенное значение, можно взять сумму пикового значения и постоянной составляющей.
При синусоидальном переменном токе используется формула:
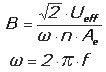
где: Uэфф — действующее значение напряжения.
Для прямоугольного сигнала формула примет вид:
![]()
где: U — пиковое напряжение.
Рассеивание тепла
Насыщение не является такой большой проблемой, как рассеивание тепла. Провода на катушках нагреваются как от постоянной, так и от переменной составляющей тока, а сердечник нагревается только от переменного тока. Следующие максимальные значения индукции (для переменного тока) могут использоваться как ориентировочные как для ферритов, так и для карбонильных сердечников:
| Частота [МГц] | 0,1 | 1 | 7 | 14 | 21 | 28 |
| Индукция макс. [mT] | 50 | 15 | 6 | 4,5 | 4 | 3 |
Там, где есть постоянный ток с переменной составляющей, например, в фильтрующих катушках источника питания, мы пренебрегли малыми потерями, пока общая плотность потока не превышает 200 мТл для большинства ферритов и 500 мТл для порошковых сердечников.
Температурная зависимость
Проницаемость феррита или порошкового сердечника сильно зависит от температуры. Обычно проницаемость увеличивается до определенной температуры (точки Кюри), где она резко падает.
Температурный коэффициент дает изменение проницаемости на К в заданном температурном диапазоне. Изменение индукции в зависимости от изменения температуры можно рассчитать по следующей формуле:
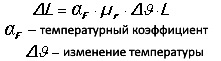
Потери также увеличиваются с повышением температуры. Когда проницаемость увеличивается, у нас более высокая магнитная индукция, а значит, тоже более высокие гистерезисные потери. Кроме того, с повышением температуры удельное сопротивление уменьшается, что приводит к увеличению потерь на вихревые токи.
Магнитные единицы
Наконец, поскольку в разных каталогах используются разные (не основные) магнитные единицы, полезно знать, как они конвертируются.
| Магнитомоторная сила | 1 G (Гилберт) = 1,257 A 1 A = 0,796 Гс. |
| Магнитный поток | 1 М (Максвелл) = 10 -8 Wb 1 Wb = 10 8 М |
| Напряженность магнитного поля | 1 Э (эрстед) = 79,6 А/м 1 А/м = 1,257 x 10 -2 Э |
| Индукция (плотность потока) | 1 Гс (гаусс) = 10 —4 Тл 1 Тл = 10 4 Гс |
Цветовой код
Не стоит заморачиваться с изготовлением катушек самостоятельно, а гораздо лучше использовать дроссель с определенной индуктивностью. Как и в случае с резисторами, для обозначения параметров дросселей используется код.
С этим способом кодирования стоит познакомиться; особенно когда нам нужно быстро найти дроссель с определенной индуктивностью в коробке с сотней других непонятных дросселей.
Итак, начнем, вот шпаргалка вам больше не понадобится.
| \ | Цифра | Множитель | Толерантность |
| серебро золото черный коричневый красный оранжевый желтый зеленый синий фиолетовый серый белый нет |
— — 0 1 2 3 4 5 6 7 8 9 — |
х10 нГн х100 нГн x1 мкГн х10 мкГн х100 мкГн x1 мГн х10 мГн х100 мГн x1 Н х10 Н х100 Н X1000 Н — |
10% 5% — 1% 2% — — 0,5% 0,25% 0,1% — — 20% |
Кодировка характеризуется четырьмя цветными полосами на внешнем эпоксидном слое:
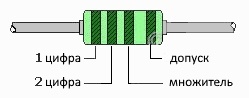
Первая полоса представляет собой первое значащее число в соответствии с таблицей выше. Вторая полоса указывает на второе значащее число. Третий столбик — множитель. Четвертая полоса — это номинальный допуск индуктивности. Если у нас есть дроссель только с тремя полосами, мы относимся к нему аналогично, а отсутствие четвертой полосы означает допуск 20%. Например, дроссель с маркировкой коричнево-красный-черный-серебристый означает 12 мкГн и допуск 10%.
Если цвета полосок плохо читаются или вы не можете определить, какая полоска первая, а какая последняя, не беспокойтесь, в таких случаях вам будет полезно узнать о серии E — большинство дросселей доступны со значениями индуктивности из Серии Е12 (то же, что и для резисторов). Считайте значение индуктивности такого дросселя и проверьте, существует ли такой дроссель в серии. Если значение, считываемое нашим значением, не существует в данной серии, это означает, что его следует читать в обратном порядке.
С Уважением, МониторБанк