Сортировка — это метод, который реализуется для упорядочения данных в определенном порядке. Сортировка необходима для того, чтобы данные, которые мы используем, находились в определенном порядке для извлечения требуемой информацию из кучи данных.
Сортировка — это метод, который реализуется для упорядочения данных в определенном порядке. Сортировка необходима для того, чтобы данные, которые мы используем, находились в определенном порядке для извлечения требуемой информацию из кучи данных.
Если данные не отсортированы, то нам придется каждый раз искать их по одному в программе, что в современном мире неприемлемо.
Таким образом, всегда рекомендуется хранить данные в определенном порядке, чтобы поиск информации, а также другие операции, выполняемые с данными, можно было выполнять быстро, легко и эффективно.
Мы всегда храним данные в виде записей. Каждая запись состоит из одного или нескольких полей. Когда каждая запись получает уникальное значение определенного поля, это называется ключевым полем. Например, в классе Roll No может быть уникальным или ключевым полем.
Мы можем отсортировать данные по определенному ключевому полю, а затем расположить их в порядке возрастания или в порядке убывания.
Точно так же в телефонном справочнике каждая запись состоит из имени человека, адреса и номера телефона. При этом номер телефона является уникальным или ключевым полем. Мы можем отсортировать данные справочника по этому телефонному полю. В качестве альтернативы мы также можем сортировать данные либо в числовом, либо в алфавитно-цифровом порядке.
Настройка данных для сортировки в самой основной памяти без какой-либо необходимости в другой вспомогательной памяти, это называется внутренней сортировкой.
А если нам нужна вспомогательная память для хранения промежуточных данных во время сортировки, то это называется техникой внешней сортировки.
В этой статье мы подробно рассмотрим различные методы сортировки в C++.
Методы сортировки
Язык C++ поддерживает различные методы сортировки, они перечислены ниже:
Пузырьковая сортировка
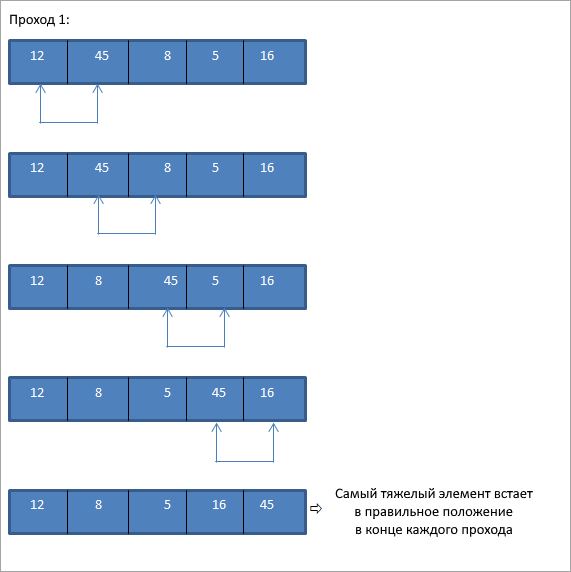
Пузырьковая сортировка (сортировка простыми обменами) — это простейший метод, при котором мы сравниваем каждый элемент с соседним элементом и меняем местами элементы, если они не в нужном нам порядке. Таким образом, в конце каждой итерации (называемой проходом) самый тяжелый (больший) элемент всплывает в конце списка.
Ниже приведен пример пузырьковой сортировки.
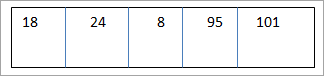
Массив для сортировки:
Как видно выше, поскольку массив небольшой и почти отсортирован, нам удалось получить полностью отсортированный массив за несколько проходов.
Давайте реализуем метод пузырьковой сортировки в скетче на C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
#include<iostream> using namespace std; int main () { int i, j,temp; int a[5] = {10,2,0,43,12}; cout <<"Input list ...\n"; for(i = 0; i<5; i++) { cout <<a[i]<<"\t"; } cout<<endl; for(i = 0; i<5; i++) { for(j = i+1; j<5; j++) { if(a[j] < a[i]) { temp = a[i]; a[i] = a[j]; a[j] = temp; } } } cout <<"Sorted Element List ...\n"; for(i = 0; i<5; i++) { cout <<a[i]<<"\t"; } return 0; } |
Вывод данных:
| Список ввода… 10 2 0 43 12 Отсортированный список элементов… 0 2 10 12 43 |
Из вывода данных видно, что в методе пузырьковой сортировки, при каждом проходе, самый тяжелый элемент встает в конце массива, тем самым полностью сортируя массив.
Сортировка выбором
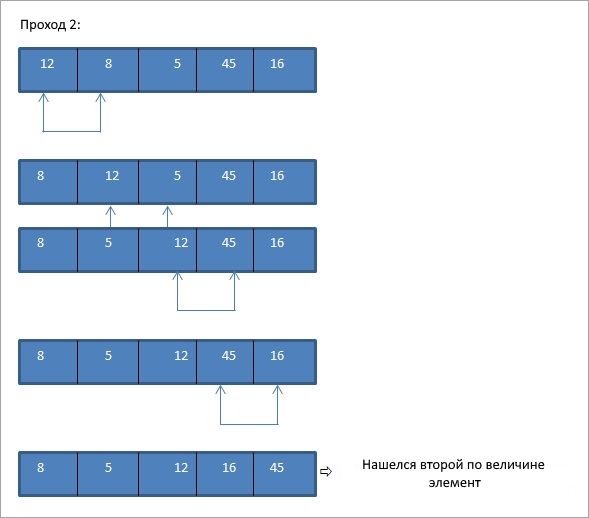
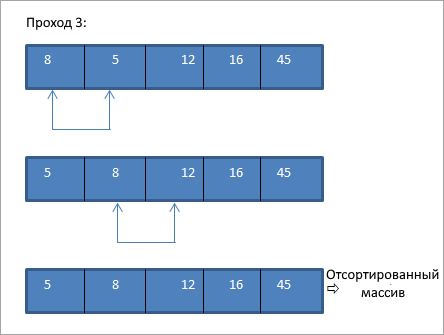
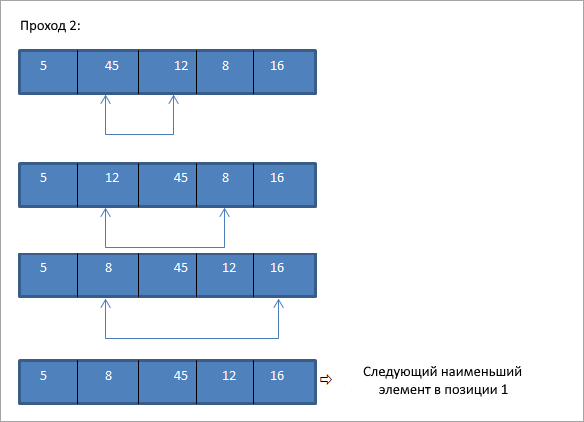
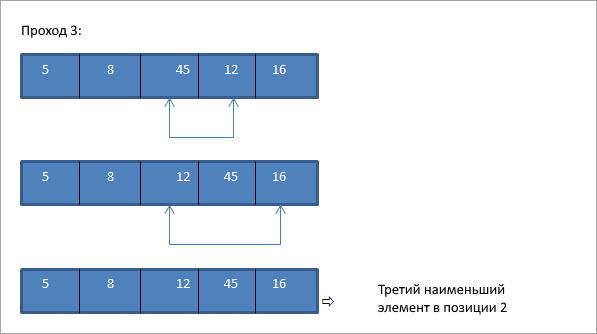
Это простая, но легко реализуемая техника, в которой мы находим наименьший элемент в списке и помещаем его на нужное место. При каждом проходе выбирается следующий наименьший элемент и помещается в правильное положение.
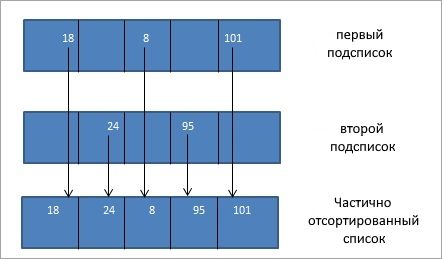
Давайте возьмем тот же массив, что и в предыдущем примере, и выполним сортировку уже выбором:
Как показано на схеме выше, для N элементов мы используем N-1 проходов, чтобы полностью отсортировать массив. В конце каждого прохода наименьший элемент массива помещается на свое место в отсортированном массиве.
Далее давайте реализуем сортировку выбором с помощью C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
#include<iostream> using namespace std; int findSmallest (int[],int); int main () { int myarray[5] = {12,45,8,15,33}; int pos,temp; cout<<"\n Input list of elements to be Sorted\n"; for(int i=0;i<5;i++) { cout<<myarray[i]<<"\t"; } for(int i=0;i<5;i++) { pos = findSmallest (myarray,i); temp = myarray[i]; myarray[i]=myarray[pos]; myarray[pos] = temp; } cout<<"\n Sorted list of elements is\n"; for(int i=0;i<5;i++) { cout<<myarray[i]<<"\t"; } return 0; } int findSmallest(int myarray[],int i) { int ele_small,position,j; ele_small = myarray[i]; position = i; for(j=i+1;j<5;j++) { if(myarray[j]<ele_small) { ele_small = myarray[j]; position=j; } } return position; } |
Вывод данных:
| Введите список элементов для сортировки 12 45 8 15 33 Отсортированный список элементов 8 12 15 33 45 |
При сортировке выбором, при каждом проходе, наименьший элемент массива помещается в правильное положение. Следовательно, в конце процесса сортировки мы получаем полностью отсортированный массив.
Сортировка вставками
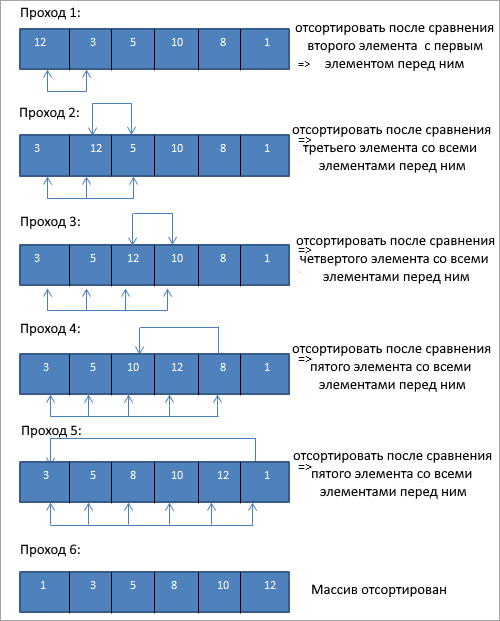
Сортировка вставками — это метод, при котором мы начинаем сортировать со второго элемента списка. Мы сравниваем второй элемент с его предыдущим (первым) элементом и помещаем его на свое место. На следующем проходе для каждого элемента мы сравниваем его со всеми предыдущими элементами и вставляем этот элемент на свое место.
Вышеупомянутые три метода сортировки просты и легко реализуемы. Эти методы хорошо работают при небольшом размере списка. По мере увеличения списка в размере, эти методы не будут работать так эффективно.
Техника будет ясна, если вы поймете следующие схемы.
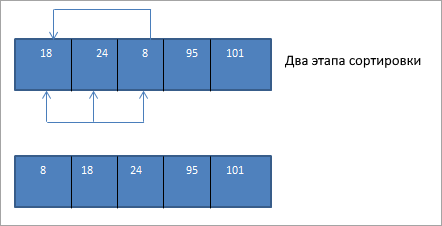
Массив для сортировки выглядит следующим образом:
Теперь для каждого прохода мы сравниваем текущий элемент со всеми его предыдущими элементами. Таким образом, в первом проходе мы начинаем со второго элемента:
Таким образом, нам требуется N проходов, чтобы полностью отсортировать массив, содержащий N элементов.
Давайте реализуем технику сортировки вставками на C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
#include<iostream> using namespace std; int main () { int myarray[5] = { 12,4,3,1,15}; cout<<"\nInput list is \n"; for(int i=0;i<5;i++) { cout <<myarray[i]<<"\t"; } for(int k=1; k<5; k++) { int temp = myarray[k]; int j= k-1; while(j>=0 && temp <= myarray[j]) { myarray[j+1] = myarray[j]; j = j-1; } myarray[j+1] = temp; } cout<<"\nSorted list is \n"; for(int i=0;i<5;i++) { cout <<myarray[i]<<"\t"; } } |
Вывод данных:
| Список ввода 12 4 3 1 15 Отсортированный список 1 3 4 12 15 |
Приведенный выше вывод данных показывает полный отсортированный массив с использованием сортировки вставками.
Быстрая сортировка
Быстрая сортировка — наиболее эффективный алгоритм, который можно использовать для сортировки данных. Этот метод использует стратегию «разделяй и властвуй», в которой задача делится на несколько подзадач и после решения этих подзадач по отдельности объединяются в полный отсортированный список.
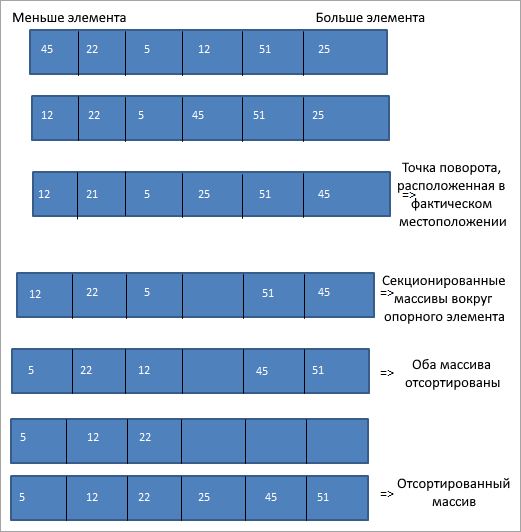
При быстрой сортировке мы сначала разделяем список вокруг опорного элемента, а затем размещаем остальные элементы на их надлежащих позициях в соответствии с этим опорным элементом.
Как показано на приведенной выше схеме, в технике быстрой сортировки мы делим массив около опорного элемента таким образом, что все элементы, меньше опорного элемента, находятся слева от него, а элементы, превышающие опорный элемент, — справа. Затем мы берем эти два массива независимо друг от друга и сортируем их, а затем объединяем их, чтобы получить результирующий отсортированный массив.
Ключом к быстрой сортировке является выбор опорного элемента. Это может быть первый, последний или средний элемент массива. Первым шагом после выбора опорного элемента является размещение опорного элемента в правильном положении, чтобы мы могли соответствующим образом разделить массив.
Давайте реализуем технику быстрой сортировки с помощью C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
#include <iostream> using namespace std; // Менять местами два элемента void swap(int* a, int* b) { int t = *a; *a = *b; *b = t; } // разделение массива, с помощью последнего элемента в качестве опорного int partition (int arr[], int low, int high) { int i = (low - 1); for (int j = low; j <= high- 1; j++) { //если текущий элемент меньше опорного //поменяйте местами элементы в точках i и j if (arr[j] <= pivot) { i++; // индекс приращения меньшего элемента swap(&arr[i], &arr[j]); } } swap(&arr[i + 1], &arr[high]); return (i + 1); } //алгоритм быстрой сортировки void quickSort(int arr[], int low, int high) { if (low < high) { //разделить массив на части int pivot = partition(arr, low, high); //сортировать вложенные массивы независимо друг от друга quickSort(arr, low, pivot - 1); quickSort(arr, pivot + 1, high); } } void displayArray(int arr[], int size) { int i; for (i=0; i < size; i++) cout<<arr[i]<<"\t"; } int main() { int arr[] = {12,23,3,43,51}; int n = sizeof(arr)/sizeof(arr[0]); cout<<"Input array"<<endl; displayArray(arr,n); cout<<endl; quickSort(arr, 0, n-1); cout<<"Array sorted with quick sort"<<endl; displayArray(arr,n); return 0; } |
Вывод данных:
| Входной массив 12 23 3 43 51 Массив, отсортированный с помощью быстрой сортировки 3 12 23 43 51 |
В приведенной выше реализации быстрой сортировки есть процедура разделения, которая используется для разбиения входного массива вокруг опорного элемента, который является последним элементом в массиве. Затем мы рекурсивно вызываем процедуру быстрой сортировки для индивидуальной сортировки подмассивов, как было показано на схеме.
Сортировка слиянием
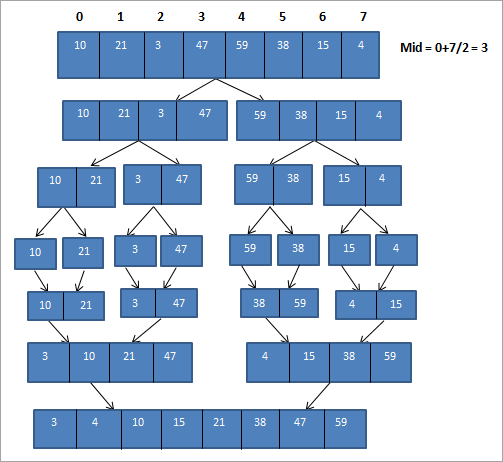
Это еще одна техника, использующая стратегию «Разделяй и властвуй». В этой технике мы сначала делим список на равные половины. Затем мы выполняем метод сортировки слиянием в этих списках независимо, чтобы оба списка были отсортированы. Наконец, мы объединяем оба списка, чтобы получить полный отсортированный список.
Сортировка слиянием и быстрая сортировка выполняются быстрее, чем большинство других методов сортировки. Их производительность остается неизменной, даже когда список становится больше.
Давайте посмотрим на приведенную схему техники сортировки слиянием:
На приведенной выше схеме видно, что метод сортировки слиянием многократно делит исходный массив на подмассивы, пока в каждом подмассиве не останется только один элемент. После этого, подмассивы сортируются независимо друг от друга и объединяются вместе, чтобы сформировать полный отсортированный массив.
Далее давайте реализуем сортировку слиянием с использованием языка C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
#include <iostream> using namespace std; void merge(int *,int, int , int ); void merge_sort(int *arr, int low, int high) { int mid; if (low < high){ //разделение массива пополам и независимое сортирование с использованием сортировки слиянием mid=(low+high)/2; merge_sort(arr,low,mid); merge_sort(arr,mid+1,high); //объединение отсортированных массивов merge(arr,low,high,mid); } } // Сортировка слиянием void merge(int *arr, int low, int high, int mid) { int i, j, k, c[50]; i = low; k = low; j = mid + 1; while (i <= mid && j <= high) { if (arr[i] < arr[j]) { c[k] = arr[i]; k++; i++; } else { c[k] = arr[j]; k++; j++; } } while (i <= mid) { c[k] = arr[i]; k++; i++; } while (j <= high) { c[k] = arr[j]; k++; j++; } for (i = low; i < k; i++) { arr[i] = c[i]; } } // считывание входного массива и вызов сортировки слиянием int main() { int myarray[30], num; cout<<"Enter number of elements to be sorted:"; cin>>num; cout<<"Enter "<<num<<" elements to be sorted:"; for (int i = 0; i < num; i++) { cin>>myarray[i]; } merge_sort(myarray, 0, num-1); cout<<"Sorted array\n"; for (int i = 0; i < num; i++) { cout<<myarray[i]<<"\t"; } } |
Вывод данных:
| Введите количество элементов для сортировки: 5 Введите 5 элементов для сортировки: 10 21 47 3 59 Отсортированный массив: 3 10 21 47 59 |
Сортировка Шелла (ракуши)
Сортировка Шелла является расширением метода сортировки вставками. В сортировке вставками мы имеем дело только со следующим элементом, тогда как в сортировке Шелла мы предоставляем приращение, с помощью которого мы создаем меньшие списки из родительского списка. Элементы в подсписках не обязательно должны быть смежными, скорее они обычно отделены друг от друга по ‘gap_value’.
Сортировка Шелла выполняется быстрее, чем сортировка вставками, и требует меньше действий:
Если мы обеспечим зазор, то у нас будут следующие подсписки с каждым элементом, который находится на расстоянии 3 элементов друг от друга.
Затем мы сортируем эти три подсписка:
Приведенный выше массив, который мы получили после объединения отсортированных подмассивов, почти отсортирован. Теперь мы можем выполнить сортировку вставками для этого массива, чтобы отсортировать весь массив.
Таким образом, мы видим, что как только мы разделим массив на подсписки, используя соответствующее приращение, а затем объединим их вместе, мы получим почти отсортированный список. Метод сортировки вставками в этом списке может быть выполнен, и массив сортируется за меньшее количество шагов, чем исходная сортировка вставками.
Ниже приведена реализация сортировки Шелла в C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
#include <iostream> using namespace std; // реализация сортировки Шелла int shellSort(int arr[], int N) { for (int gap = N/2; gap > 0; gap /= 2) { for (int i = gap; i < N; i += 1) { //сортировка подсписков, созданных с помощью gap int temp = arr[i]; int j; for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) arr[j] = arr[j - gap]; arr[j] = temp; } } return 0; } int main() { int arr[] = {45,23,53,43,18}; //Вычисление размера массива int N = sizeof(arr)/sizeof(arr[0]); cout << "Array to be sorted: \n"; for (int i=0; i<N; i++) cout << arr[i] << " "; shellSort(arr, N); cout << "\nArray after shell sort: \n"; for (int i=0; i<N; i++) cout << arr[i] << " "; return 0; } |
Вывод данных:
| Массив для сортировки: 45 23 53 43 18 Массив после сортировки Шелла: 18 23 43 45 53 |
Таким образом, сортировка Шелла действует как огромное улучшение по сравнению с сортировкой вставками и даже не требует половины шагов для сортировки массива.
Пирамидальная сортировка (сортировка кучей)
Пирамидальная сортировка — это метод, в котором структура данных кучи (min-heap или max-heap) используется для сортировки списка. Сначала мы создаем кучу из несортированного списка, а также используем кучу для сортировки массива.
Пирамидальная сортировка эффективна, но не так быстра, как сортировка слиянием:
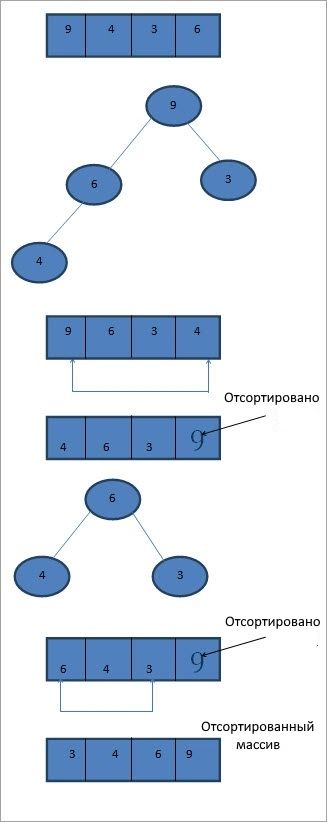
Как показано на схеме выше, мы сначала создаем максимальную кучу из элементов массива, которые нужно отсортировать. Затем мы проходим по куче и меняем местами последний и первый элемент. В это время последний элемент уже отсортирован. Затем мы снова строим максимальную кучу из оставшихся элементов.
Снова обходим кучу и меняем местами первый и последний элементы и добавляем последний элемент в отсортированный список. Этот процесс продолжается до тех пор, пока в куче не останется только один элемент, который станет первым элементом отсортированного списка.
Теперь давайте реализуем сортировку кучей с помощью C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
#include <iostream> using namespace std; // Функция дерева void heapify(int arr[], int n, int root) { int largest = root; // корень - самый большой элемент int l = 2*root + 1; // слева = 2*корень + 1 int r = 2*root + 2; // справа = 2*корень + 2 // Если левый дочерний элемент больше корневого if (l < n && arr[l] > arr[largest]) largest = l; // Если правый дочерний элемент больше, чем самый большой на данный момент if (r < n && arr[r] > arr[largest]) largest = r; // Если самый большой не является корневым if (largest != root) { //поменять местами корневой и самый большой swap(arr[root], arr[largest]); // Рекурсивное наращивание поддерева heapify(arr, n, largest); } } // реализация сортировки кучи void heapSort(int arr[], int n) { // создать кучу for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // извлечение элементов из кучи один за другим for (int i=n-1; i>=0; i--) { // Переместить текущий корень в конец swap(arr[0], arr[i]); // снова вызвать max heapify для уменьшенной кучи heapify(arr, i, 0); } } /* print contents of array - utility function */ void displayArray(int arr[], int n) { for (int i=0; i<n; ++i) cout << arr[i] << " "; cout << "\n"; } // основная программа int main() { int heap_arr[] = {4,17,3,12,9}; int n = sizeof(heap_arr)/sizeof(heap_arr[0]); cout<<"Input array"<<endl; displayArray(heap_arr,n); heapSort(heap_arr, n); cout << "Sorted array"<<endl; displayArray(heap_arr, n); } |
Вывод данных:
| Входной массив: 4 17 3 12 9 Отсортированный массив: 3 4 9 12 17 |
Вот мы и обсудили все основные методы сортировки со всеми приложенными схемами. Мы подробно изучим каждую из этих техник в наших следующих статьях вместе с различными примерами, чтобы еще лучше понять каждую технику.
Итог
Сортировка необходима для того, чтобы данные находились в правильном порядке. Доступ к неотсортированным данным может занять больше времени и, таким образом, может снизить производительность всей программы. Значит, для любых операций, связанных с данными, таких как доступ, поиск, манипулирование и т. д., нам нужно, чтобы данные были отсортированы.
В программировании используется множество методов сортировки. Каждый метод может использоваться в зависимости от структуры данных, которую мы используем, или времени, затрачиваемого алгоритмом на сортировку данных, или объема памяти, используемого алгоритмом для сортировки данных. Метод, который мы должны использовать, также зависит от того, какую структуру данных мы сортируем.
Методы сортировки позволяют нам сортировать наши структуры данных в определенном порядке и располагать элементы в порядке возрастания или убывания. Мы рассказали подробно вам о таких методах сортировки, как сортировка пузырьком, сортировка выбором, сортировка вставками, быстрая сортировка, сортировка Шелла и сортировка слиянием. Пузырьковая сортировка и сортировка выбором проще в реализации.
В нашей последующей статье мы подробно рассмотрим технику пузырьковой сортировки в C++.
С Уважением, МониторБанк