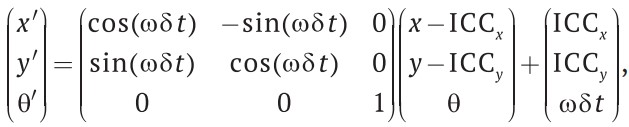В предыдущей статье «Начало работы с операционной системой для робота (ROS)» мы познакомились с основными понятиями и установкой операционной системы роботов ROS и с программой – имитатором робота Gazebo. Как ранее уже упоминалось, цель этой серии статей – помочь читателю создать автономный мобильный робот с нуля. Перемещаться этот робот будет с помощью колес. Проектируемый нами робот будет оснащен двумя ведущими колесами, которые мы установим на противоположных сторонах шасси. Управлять направлением движения мы будем с помощью разности скорости вращения ведущих колес. Например, если скорость вращения правого колеса будет меньше, чем скорость вращения левого, робот будет поворачивать вправо, и наоборот, если правое колесо будет вращаться быстрее левого, робот будет поворачивать влево.
В предыдущей статье «Начало работы с операционной системой для робота (ROS)» мы познакомились с основными понятиями и установкой операционной системы роботов ROS и с программой – имитатором робота Gazebo. Как ранее уже упоминалось, цель этой серии статей – помочь читателю создать автономный мобильный робот с нуля. Перемещаться этот робот будет с помощью колес. Проектируемый нами робот будет оснащен двумя ведущими колесами, которые мы установим на противоположных сторонах шасси. Управлять направлением движения мы будем с помощью разности скорости вращения ведущих колес. Например, если скорость вращения правого колеса будет меньше, чем скорость вращения левого, робот будет поворачивать вправо, и наоборот, если правое колесо будет вращаться быстрее левого, робот будет поворачивать влево.
Эта статья поможет вам провести математический анализ движения робота и решить уравнение кинематики робота. Уравнение кинематики даст вам возможность с помощью данных, получаемых от датчиков робота, предсказать его положение во время движения.
В этой статье будут рассмотрены следующие темы:
- математическое моделирование робота;
- введение в систему дифференциального привода и кинематику робота;
- инверсная кинематика.
Математическое моделирование робота
Наиболее важная часть мобильного робота – это система управления. С помощью нее робот ориентируется и перемещается в пространстве. Одной из самых простых и рентабельных систем управления является система дифференциального привода. Дифференциальный привод состоит из двух независимых друг от друга ведущих колес, установленных на общей оси. Каждое ведущее колесо приводится в движение отдельным двигателем. Дифференциальный привод – это неголономная система, которая имеет ограничения в изменении положения робота. Примером неголономной системы является автомобиль, поскольку он не может изменить положение без изменения
позы. Таким образом, имея три степени свободы (3D), автомобиль с помощью газа, тормоза и рулевого управления может использовать только две степени свободы (2D).
Напомним, голономная система – это механическая система, все механические связи которой можно свести к геометрическим. Такие связи накладывают ограничения только на положение системы, но не на величины скоростей.
Механической связью называют ограничения, накладываемые на координаты и скорости механической системы, которые должны выполняться на любом ее движении.
Если все кинематические связи нельзя свести к геометрическим связям, то данная система будет неголономной. Таким образом, неголономная система – это механическая система, на которую, кроме геометрических связей, наложены еще и дифференциальные (кинематические). Их нельзя свести к геометрическим связям.
Далее мы рассмотрим работу робота с дифференциальным приводом и возможность смоделировать его математически.
Введение в систему дифференциального привода и кинематику робота
Кинематика – изучение движения объекта с точки зрения математики. Она рассматривает движение объекта без учета влияющих на него внешних сил. Здесь в основном внимание привлекает геометрическое отношение деталей, обеспечивающих управление конструкцией. Динамика – это исследование движения объекта с учетом всех сил, влияющих на робота.
Мобильный робот имеет шесть степеней свободы (DOF). Три степени свободы: х, у и z — связаны с тремя координатными осями, позволяющими определить положение объекта в трехмерном пространстве. Остальные три степени свободы относятся к ориентации робота в пространстве. Это такие значения, как крен (боковой наклон, или раскачивание корпуса робота относительно оси движения), тангаж (наклон аппарата относительно горизонтальной поперечной оси, т. е. наклон вниз или подъем вверх передка робота) и рыскание (небольшие изменения направления движения аппарата вправо или влево относительно его курса). Робот с дифференциальным приводом перемещается в двухмерной плоскости (2D), и его положение в любой момент можно описать двумя глобальными координатами Х и Y, лежащими в горизонтальной плоскости. При этом курс робота обозначается как θ. Этих данных вполне достаточно, чтобы описать положение робота с дифференциальным приводом.
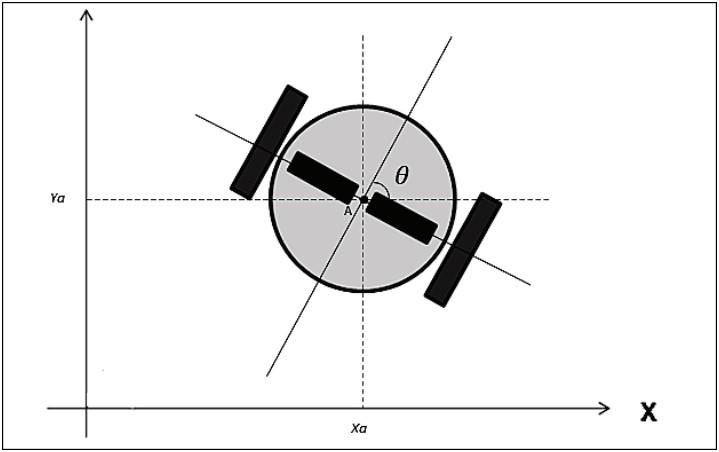
Как уже говорилось ранее, дифференциальный привод робота основан на разности между скоростью вращения правого и левого ведущих колес. Если скорость вращения ведущих колес одинакова, робот движется прямо. При изменении скорости вращения одного ведущего колеса относительно другого робот будет выполнять поворот в ту сторону, в которой скорость вращения ведущего колеса меньше по отношению ко второму ведущему колесу. Ниже на фото представлена пара популярных роботов с дифференциальным приводом:


Прямая кинематика дифференциального робота
С помощью уравнений кинематики для робота с дифференциальным приводом определяется положение устройства. Представим, что начальное положение робота в момент времени t – X, Y, θ. Нам требуется определить, какое положение устройство займет (X′, Y′, θ′) за промежуток времени t + dt. При этом следует учесть следующие параметры: v-left – скорость левого и v-right – скорость правого колеса.
Эта методика расчета положения используется для проводки робота по требуемой траектории.
Объяснение уравнений прямой кинематики
Объяснение уравнения кинематики мы можем начать с формулирования решения для движения робота вперед без учета его массы и действующих на объект сил. Показанное ниже фото иллюстрирует кинематику одного из колес робота:
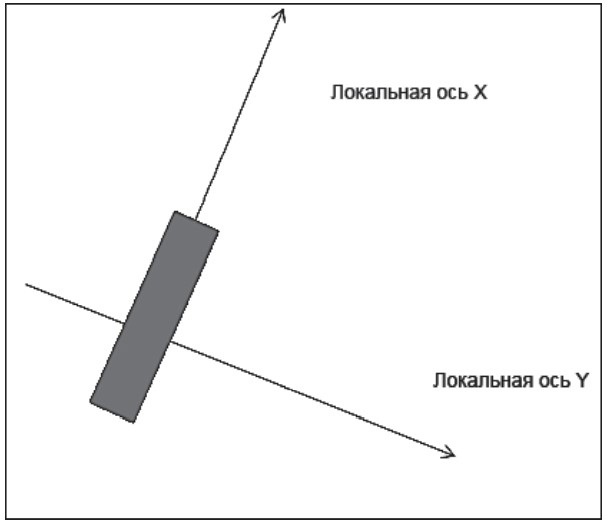
Наклон вправо или влево относительно оси Y называется креном; все остальное можно рассматривать как скольжение. Предположим, что колесо не проскальзывает. В этом случае за один оборот обод колеса пройдет расстояние, равное 2πr, где r – радиус колеса. Будем считать, что движение происходит в двухмерной плоскости с плоской ровной поверхностью. Выполняя поворот, робот будет поворачиваться вокруг точки, находящейся на оси, совпадающей с осью правого и левого ведущих колес. Эта точка находится за пределами робота и называется мгновенным центром кривизны (ICC). На следующем фото вы увидите конфигурацию ведущих колес робота с дифференциальным приводом по отношению к точке мгновенного центра кривизны (ICC).
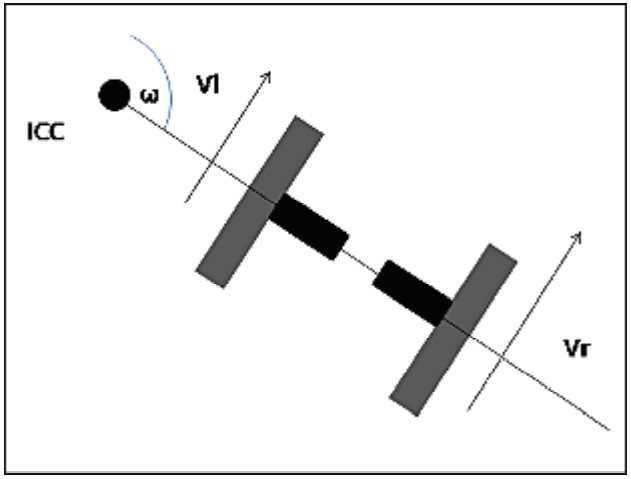
Основное понятие, без которого не получится вывести уравнение кинематического привода, – это угловая скорость робота, обозначаемая буквой w. При повороте ведущие колеса робота катятся по окружности, центр которой совпадает с мгновенным центром кривизны (ICC). Скорость колеса описывается формулой v = 2πr/T, где T – время, затраченное на прохождение колесом расстояния, равного длине полной окружности с центром, совпадающим с точкой ICC. Угловая скорость w определяется как 2π/T и измеряется в радианах (градусах) в секунду. Радиан – это угол, соответствующий дуге, длина которой равна радиусу этой дуги. 1 радиан равен 57,3°.
Если объединить уравнения для расчета скорости колеса v и его угловой скорости w, получим уравнение w = 2π/T.
v = rw. (1)
(уравнение линейной скорости)
Схема дифференциального привода показана на следующем фото:
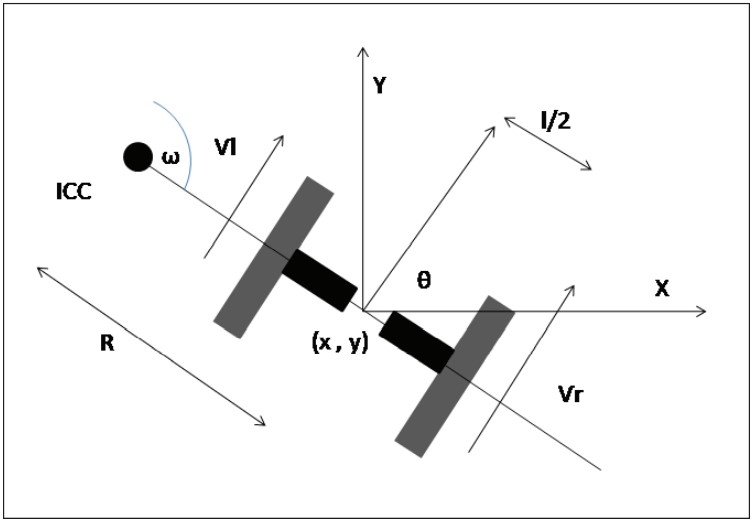
Если применить предыдущее уравнение к обоим ведущим колесам, результат будет одинаковым, т. е. w:
w(R + l/2) = Vr. (2)
w(R – l/2) = Vl. (3)
(уравнение дифференциального привода колес робота)
При этом R – расстояние между ICC и центром оси, проходящей через колеса, а l – длина оси колеса. Преобразовав выражения w и R, мы получим следующий результат:
R = l/2(Vl + Vr)/(Vr – Vl); (4)
w = (Vr – Vl)/l. (5)
(уравнение для вычисления расстояния от ICC до центра оси робота и расчета угловой скорости робота)
Предыдущие уравнения позволяют решать поставленные перед нами задачи кинематики. Предположим, что робот движется с угловой скоростью в течение wt секунд. В этом случае траектория движения и направление робота изменятся:
q′ = wdt + q. (6)
(уравнение для расчета изменения траектории движения)
Центр вращения ICC определяется базовой тригонометрией:
ICC = [ICCx, ICCy] = [x – Rsinq, y + Rcosq]. (7)
(уравнение для поиска ICC)
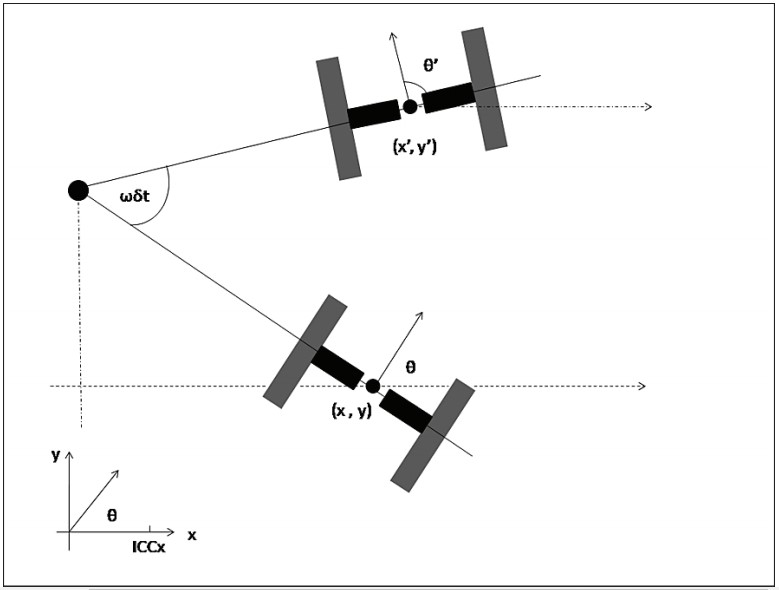
С учетом стартовой позиции (x, y) новое положение (х′, y′) может быть вычислено с помощью 2D-матрицы вращения. Учитывая движение робота с угловой скоростью ω в течение δt секунд относительно точки ICC, мы получим следующую позицию для времени t + δt:
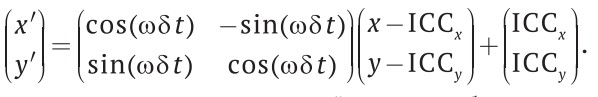
(8)
(уравнение для вычисления новой позиции робота)
Учитывая ω, δt и R, новое положение робота (х′, y′ и θ′) можно вычислить с помощью уравнений (6) и (8). Угловая скорость ω вычисляется с помощью уравнения (5); точно измерить скорости Vr и Vl затруднительно.
Вместо непосредственного вычисления скорости колеса можно измерить его реальную скорость. Измерение реальной скорости производится с помощью энкодера. Энкодер – датчик, преобразующий подконтрольную величину в электрический сигнал. В нашем случае энкодер для определения угла поворота колеса вокруг своей оси фиксирует импульсы. Угол поворота колеса определяется количеством зафиксированных импульсов. В качестве рабочей величины применяется количество импульсов на один полный оборот колеса. Значениями одометрии робота являются данные от колесных энкодеров. Энкодеры установлены на осях колеса и передают двоичные сигналы для каждого шага вращения колеса (каждый шаг (step) равен 0,1 мм). Сигналы от энкодеров,
полученные за временной промежуток от t до t + δt, подаются на счетчик импульсов, в результате чего можно вычислить пройденное расстояние vδt:
n×step = vdt.
Здесь n – количество импульсов, зафиксированных энкодером за заданное время.
Из этого можно вычислить v:
v = n×step/ dt. (9)
(уравнение для вычисления линейной скорости с помощью данных энкодера)
Если мы подставим уравнение (9) в уравнения (3) и (4), то получим следующий результат:
R = l/2(Vl + Vr)/(Vr – Vl) = l/2(nl + nr)/(nr – nl); (10)
wdt = (Vr – Vl)dt/l = (nr – nl)×step/l. (11)
(уравнение для вычисления R с помощью данных, полученных от энкодера)
Здесь nl и nr – количество импульсов, полученных от энкодеров левого и правого колес. Vl и Vr – это скорости левого и правого колес. Итак, робот перемещается с позиции (x, y, θ) в позицию (х′, y′, θ′). При этом от датчиков левого и правого колес в течение времени δt соответственно поступит nl и nr импульсов. В этом случае новое положение робота определяется по формуле:
(12)
(уравнение для вычисления положения робота с помощью данных, полученных от датчиков правого и левого колес)
где
R = l/2(nl + nr)/(nr – nl); (13)
wdt = (nr – nl)×step/l; (14)
ICC = [x – Rsinq, y + Rcosq]. (15)
(уравнение для вычисления ICC и других параметров с помощью данных,
полученных от датчиков правого и левого колес)
Полученное кинематическое уравнение в основном зависит от конструкции и размеров деталей ходовой части робота. Изменение конструкции может привести к корректировке уравнений.
Обратная кинематика
C помощью уравнений прямой кинематики мы можем определить новое положение робота, учитывая скорость вращения колеса. Теперь можно приступить к обратной задаче.
Допустим, робот в момент времени t находится в положении (х, y, θ). Определим скорости левого (V-left) и правого (V-right) колес так, что за промежуток времени t + δt робот займет новое положение с координатами (х′, y′ и θ′).
В устройствах с дифференциальным приводом переместить робота в нужную позицию с помощью только простой установки скорости вращения колес нельзя. Как уже упоминалось ранее, дифференциальный привод – это неголономная механическая система, в которой, кроме геометрических, учитываются и кинематические связи. Неголономная система накладывает некоторые ограничения на управление роботами.
Для увеличения степени подвижности (управляемости) неголономного робота следует использовать разность скоростей левого и правого колес. Если вставить значения из уравнений (12) в уравнение (15), то можно определить способы управления, которые в дальнейшем сможем запрограммировать:
- если V-left = V-right, => nr = nl => R = ∞, wdT = 0 (т. е. скорость и направление вращения левого ведущего колеса совпадают со скоростью и направлением вращения правого колеса), значит, робот движется прямолинейно и q остается неизменной;
- если V-left = –V-right, => nr = –nl, => R = 0, wdT = 2nl × step/l и ICC = [ICCx, ICCy] = [x, y] => x′ = x, y′ = y, θ′ = θ + ωδt => (т. е. скорости вращения левого и правого колес одинаковы, но направления их вращения не совпадают, колеса вращаются навстречу друг другу), значит, робот вращается вокруг мгновенного центра кривизны (ICC), т. е. ∀q может изменяться без ограничений при неизменных координатах [x, y].
Объединяя приведенные ниже способы управления, можно создать алгоритм, позволяющий достичь любого положения робота относительно его начального положения:
1) поворачивайте, пока ориентация робота не совпадет с линией, ведущей из исходного в целевое положение, V-right = –V-left = V-rot (скорость поворота);
2) двигайтесь прямо до тех пор, пока положение робота не совпадет с целевым положением, V-right = V-left = V-ahead (скорость прямого движения);
3) поворачивайте, пока ориентация робота не совпадет с ориентацией цели, V-right = –V-left = V-rot. Скорости V-rot и V-ahead выбираются произвольно.
Итоги
Эта статья была посвящена не только фундаментальным концепциям роботов с дифференциальным приводом, но и кинематическим уравнениям движения таких устройств. В начале статьи были рассмотрены основы дифференциального привода роботов. Далее мы вывели использующиеся в таких устройствах уравнения прямой кинематики и объяснили их с помощью кинематических схем. Затем познакомились с уравнениями обратной кинематики. В следующей статье «Моделирование робота с дифференциальным приводом» рассмотрим, как с помощью ROS и Gazebo создать модель автономного мобильного робота.
За основу данной статьи взята книга Д. Лентина «Изучение робототехники с использованием Python»
С Уважением, МониторБанк