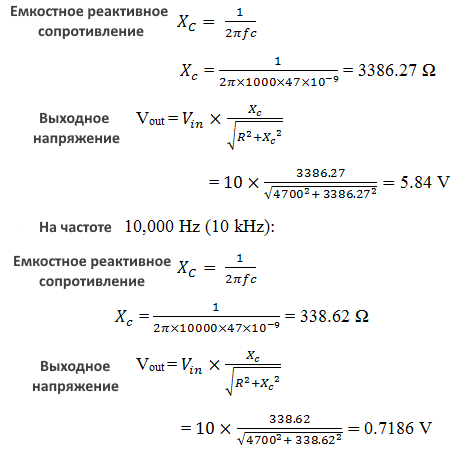В этой статье мы поговорим о пассивных RC-фильтрах низких частот. Как следует из названия, это фильтр низких частот, разработанный с использованием пассивных компонентов. В последующих статьях мы вам расскажем об основной схеме пассивных RC-фильтров низких частот, их частотной характеристике, выходном напряжении, их применениях и о многом другом.
Чтобы получить информацию о пассивных RC-фильтрах высоких частот, прочитайте статью «Пассивные RC-фильтры высоких частот».
Фильтр — это схема, которая используется для фильтрации сигналов, то есть данный фильтр будет пропускать только необходимые сигналы и избегать нежелательных сигналов. Обычно фильтры собраны либо с применением пассивных компонентов, либо с применением активных компонентов:
Пассивными компонентами являются резисторы, катушки индуктивности и конденсаторы.
Активными компонентами являются транзисторы, полевые транзисторы и операционные усилители.
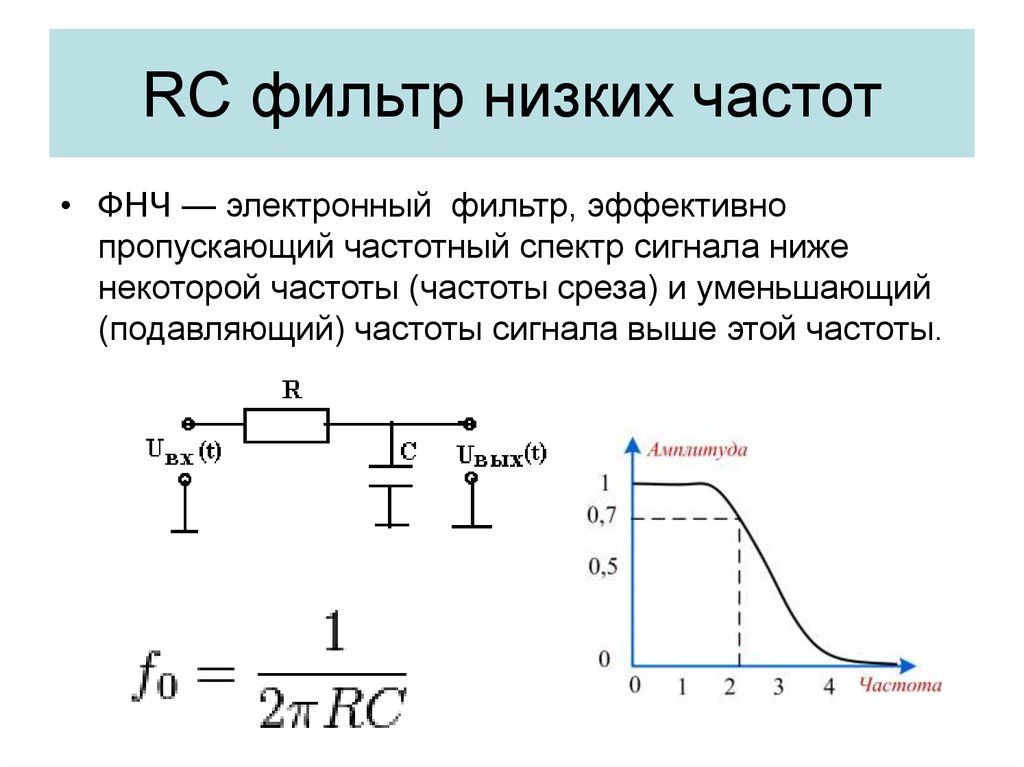
Фильтр низких частот — это фильтр, который пропускает только низкочастотные сигналы и ослабляет или останавливает высокочастотные сигналы. Он позволяет сигналам только от 0 Гц отключать частоту ‘fc’. Это значение частоты среза будет зависеть от значения компонентов, используемых в схеме.
Обычно эти фильтры ниже частоты 100 кГц. Частота среза называется частотой прерывания или частотой переключения.
Пассивный фильтр низких частот
Схема фильтра низких частот, разработанная с помощью пассивных компонентов, называется пассивным фильтром низких частот.
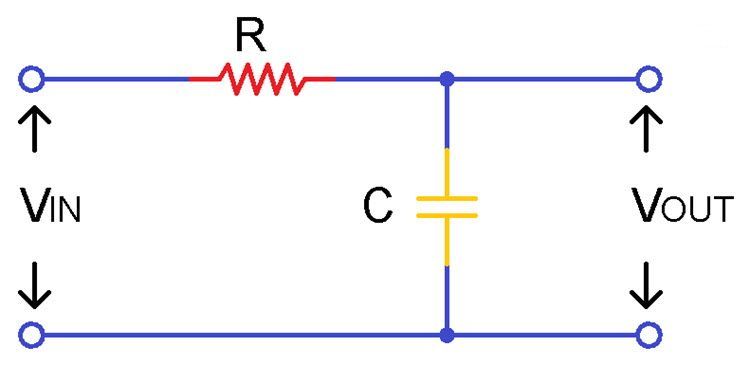
Ниже показана простая схема RC-фильтра низких частот:
Простое последовательное подключение резистора ‘R’ к конденсатору ‘C’ дает RC фильтр низких частот. Его можно просто назвать фильтром низких частот (ФНЧ). Резистор не зависит от изменений приложенных частот в цепи, но конденсатор является чувствительным компонентом, что означает, что он реагирует на изменения в цепи.
Поскольку эта схема имеет только один реактивный компонент, ее также можно назвать ‘однополюсным фильтром» или «фильтром первого порядка». Входное напряжение ‘Vin’ последовательно подается на резистор, а выходное напряжение снимается только с конденсатора.
Поскольку конденсатор является чувствительным компонентом, основная концентрация, которую необходимо соблюдать, — это “емкостное реактивное сопротивление”. Емкостное реактивное сопротивление — это противодействующий отклик, создаваемый конденсатором в цепи.
Для поддержания емкости конденсатора, конденсатор будет противостоять небольшому току, протекающему в цепи. Это противодействие протеканию тока в цепи называется импедансом. Таким образом, емкостное реактивное сопротивление уменьшается с увеличением встречного тока.
Значит, мы можем сказать, что емкостное реактивное сопротивление обратно пропорционально частоте, подаваемой на схему. Значение резистивного сопротивления резистора стабильно, тогда как значение емкостного реактивного сопротивления изменяется. Падение напряжения на конденсаторе намного меньше по сравнению с потенциалом напряжения конденсатора.
Это означает, что на низких частотах падение напряжения мало, а потенциал напряжения большой, но на высоких частотах падение напряжения очень высокое, а потенциал напряжения меньше. Благодаря этому явлению мы можем сказать, что вышеупомянутая схема может действовать как схема «частотно-регулируемого делителя напряжения».
Емкостное реактивное сопротивление может быть сформулировано следующим образом:
Расчет выходного напряжения
Чтобы получить уравнение делителя потенциала, мы должны учитывать полное сопротивление, емкостное сопротивление, входное и выходное напряжение. Используя эти термины, мы можем сформулировать уравнение для делителя потенциала RC следующим образом:
Используя это уравнение, мы можем рассчитать значение выходного сигнала на любой применяемой частоте.
Пример фильтра низких частот
Давайте возьмем значения выходного напряжения и значения емкостного сопротивления, рассмотрев значения резисторов и конденсаторов. Пусть значение резистора R равно 4,7 Ком, а значение конденсатора равно 47 нФ. Подаваемое входное напряжение переменного тока составляет 10 В. Значения частот составляют: 1 кГц и 10 кГц:
Таким образом, мы можем четко сказать, что при увеличении частоты емкостное реактивное сопротивление уменьшается. Уменьшается не только емкостное сопротивление, но и выходное напряжение.
Из приведенного выше примера видно, что емкостное реактивное сопротивление уменьшается с 3386, 27 Ом до 338,62 Ом, тогда как выходное напряжение уменьшается с 5,84 вольт до 0,718 вольт с увеличением частоты с 1 кГц до 10 кГц.
Частотная характеристика фильтра низких частот
Вы должны знать, что величина |H(jw)| фильтра принимается за коэффициент усиления схемы. Это усиление измеряется как 20 log (V out / V in), и для любой RC-схемы угол наклона составляет -20 дБ.
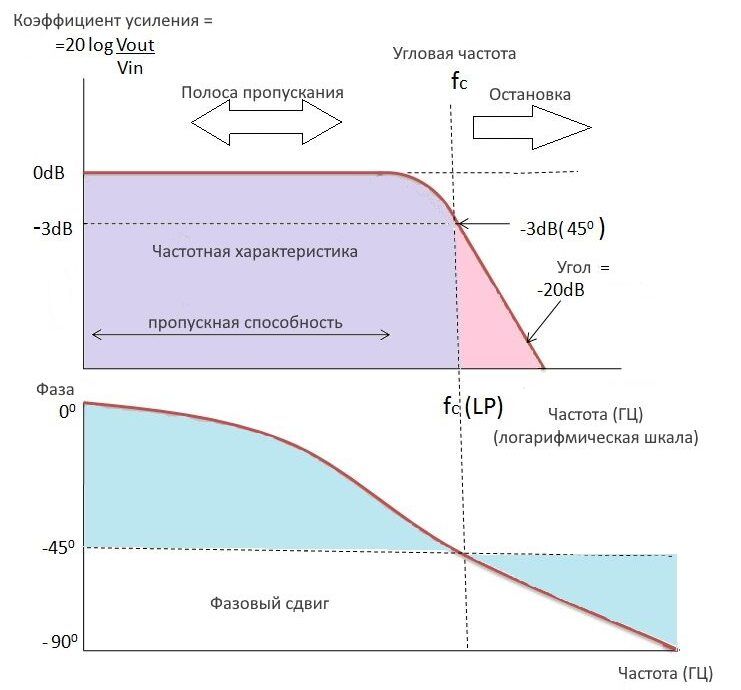
Полоса частот ниже области среза называется «полосой пропускания», а полоса частот после частоты среза называется «полосой заграждения’. Из графика можно заметить, что полоса пропускания представляет собой полосу пропускания фильтра.
Из этого графика видно, что до частоты среза коэффициент усиления постоянен, потому что выходное напряжение пропорционально значению частоты на низких частотах. Это связано с емкостным реактивным сопротивлением, которое действует как разомкнутая цепь на низких частотах и обеспечивает максимальный ток через цепь на высоких частотах. Значение емкостного сопротивления очень велико на низких частотах, поэтому оно обладает большей способностью блокировать протекание тока через цепь.
Как только оно достигает значения частоты среза, выходное напряжение постепенно уменьшается и достигает нуля. Коэффициент усиления также уменьшается вместе с выходным напряжением. После частоты среза отклик наклона схемы достигнет точки спада, которая происходит при -20 дБ.
В основном это связано с увеличением частоты, при увеличении частоты значение емкостного сопротивления уменьшается, и, следовательно, уменьшается способность блокировать ток через конденсатор. Когда ток через цепь увеличивается и из-за ограниченной емкости конденсатора цепь действует как при коротком замыкании. Таким образом, выходное напряжение фильтра равно нулю на высоких частотах.
Единственный способ избежать этой проблемы — выбрать частотные диапазоны, до которых могут выдержать резистор и конденсатор. Значения конденсатора и резистора играют главную роль, потому что от этих значений зависит только частота среза ‘fc’. Если диапазоны частот находятся в пределах диапазона частот среза, мы можем решить проблему короткого замыкания.
Эта точка отсечения возникает, когда значение сопротивления и значение емкостного реактивного сопротивления совпадают, что означает, что векторная сумма сопротивления и реактивной емкости равны, то есть, когда R = xc и в этой ситуации входной сигнал ослабляется на -3 дБ.
Это затухание составляет приблизительно 70,7% от входного сигнала. Время, необходимое для зарядки и разрядки пластин конденсатора, изменяется в зависимости от синусоидальной волны. Из-за этого фазовый угол (ø) выходного сигнала отстает от входного сигнала после частоты среза. На частоте среза выходной сигнал не совпадает по фазе на -45°.
Если частота входного сигнала фильтра увеличивается, угол задержки выходного сигнала схемы увеличивается. Просто при большем значении частоты схема больше не в фазе.
Конденсатору нужно больше времени для зарядки и разрядки пластин на низких частотах, поскольку время переключения синусоидальной волны больше. Но с увеличением частоты, время, необходимое для переключения на следующий импульс, постепенно уменьшается. Из-за этого возникают временные колебания, которые приводят к сдвигу фазы выходной волны.
Частота среза пассивного фильтра низких частот в основном зависит от значений резисторов и конденсаторов, используемых в схеме фильтрации. Эта частота отсечки обратно пропорциональна значениям резисторов и конденсаторов. Частота среза пассивного фильтра низких частот задается как:
fC = 1/(2πRC)
Сдвиг фазы пассивного фильтра низких частот задается как:
Сдвиг фазы (ø) = – tan-1 (2πfRc)
Постоянная времени (τ)
Как мы уже говорили, время, затрачиваемое конденсатором на зарядку и разрядку пластин относительно входа синусоидальной волны, что приводит к разности фаз. Резистор и конденсатор в последовательном соединении будут производить эффект зарядки и разрядки.
Постоянная времени последовательной RC-схемы определяется как время, затрачиваемое конденсатором на зарядку до 63,2% от конечного установившегося значения, а также определяется как время, затрачиваемое конденсатором на разрядку до 36,8% от установившегося значения. Эта постоянная времени представлена символом ‘τ’.
Соотношение между постоянной времени и частотой среза выглядит следующим образом:
Постоянная времени τ = RC = 1/ 2πfc and ωc = 1/τ = 1/RC
Таким образом, мы можем сказать, что выходной сигнал фильтра зависит от частот, подаваемых на вход, и от постоянной времени.
Пассивный фильтр низких частот: пример 2
Давайте вычислим частоту среза фильтра низких частот, который имеет сопротивление 4,7 К и емкость 47 Нф.
Вы уже знаете, что уравнение для частоты среза имеет вид:
fc = 1/2πRC = 1/(2π x 4700 x 47 x 10-9) = 720 Hz
Пассивный фильтр низких частот второго порядка
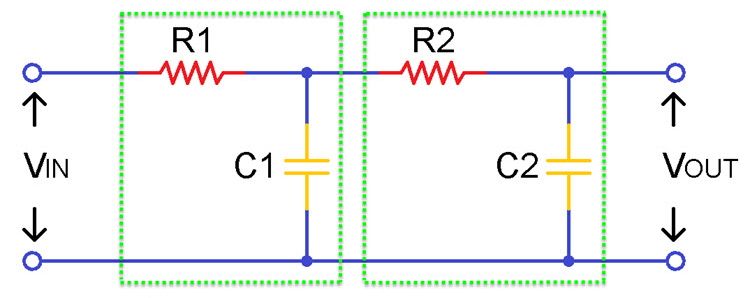
До сих пор мы рассматривали только фильтр низких частот первого порядка, который собирается путем последовательного подключения резистора и конденсатора. Однако иногда одного каскада может быть недостаточно для удаления всех нежелательных частот, тогда используются фильтры второго порядка. Схема показана ниже:
RC-фильтр низких частот второго порядка может быть получен простым добавлением еще одной ступени к фильтру низких частот первого порядка. Этот фильтр дает наклон -40 дБ или -12 дБ, а фильтр четвертого порядка дает наклон -80 дБ и так далее.
Коэффициент усиления пассивного фильтра низких частот на частоте среза задается как:
A = (1/√2)n
Где n — порядок или количество ступеней
Частота среза фильтра низких частот второго порядка задается как:
fc = 1/ (2π√(R1C1R2C2))
Фильтр низких частот второго порядка — частота 3 дБ задается как:
f (-3dB) = fc √ (2(1/n) – 1)
Где fc — частота среза, n — количество ступеней и ƒ- 3 дБ частота полосы пропускания.
Краткое описание фильтров низких частот
Фильтр низких частот состоит из резистора и конденсатора. Не только конденсатор, но и любой реактивный компонент с резистором обеспечивает фильтр низких частот. Это фильтр, который пропускает только низкие частоты и ослабляет высокие частоты.
Частоты ниже частоты среза называются частотами полосы пропускания, а частоты, превышающие частоту среза, называются частотами полосы заграждения. Полоса пропускания — это ширина полосы фильтра.
Частота отключения фильтра будет зависеть от значений компонентов, выбранных для проектирования схемы. Частоту среза можно рассчитать, используя приведенную ниже формулу:
fC = 1/(2πRC)
Коэффициент усиления фильтра принимается как величина фильтра, и коэффициент усиления может быть рассчитан с использованием формулы 20 log (Vout / Vin). Выходной сигнал фильтра остается постоянным до тех пор, пока уровни частоты не достигнут предельной частоты.
При частоте среза выходной сигнал составляет 70,7% от входного сигнала, а после частоты среза выходной сигнал постепенно уменьшается до нуля. Фазовый угол выходного сигнала отстает от входного сигнала после частоты среза.
На частоте среза сдвиг фазы выходного сигнала составляет 45°.
Если мы поменяем местами положения резистора и конденсатора в цепи фильтра низких частот, то схема будет вести себя как фильтр верхних частот.
Для синусоидальных входных волн схема ведет себя как фильтр низких частот первого порядка. Но когда изменяется тип входного сигнала, необходимо учитывать, что происходит с выходом фильтра.
Когда мы меняем тип входного сигнала либо на режим переключения (ВКЛ / ВЫКЛ), либо на прямоугольную волну, схема ведет себя как интегратор.
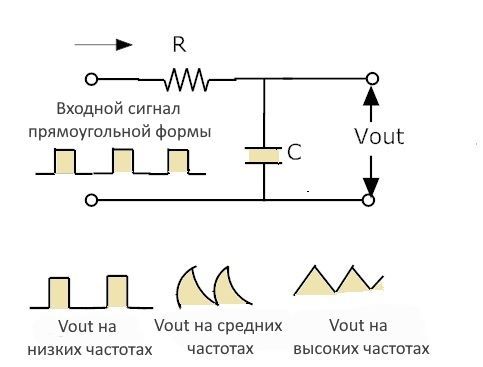
Фильтр низких частот как схема формирования волны
На приведенной выше схеме показана производительность фильтра для квадратного ввода. Когда вход фильтра низких частот представляет собой прямоугольную волну, то полученный выходной сигнал фильтра будет иметь треугольную форму.
Это связано с тем, что конденсатор не может действовать как переключатель включения или выключения. На низких частотах, когда вход фильтра прямоугольный, выходной сигнал также будет только прямоугольный.
Когда частота увеличивается, выходной сигнал фильтра выглядит как треугольная волна. Тем не менее, если мы увеличим частоту, амплитуда выходного сигнала уменьшится.
Треугольная волна генерируется из-за действия конденсаторов или просто схема зарядки и разрядки конденсатора приводит к треугольной волне.
Итог
Основное назначение схем фильтров низких частот — избегать пульсаций переменного тока на выходе выпрямителя. Фильтр низких частот используется в схемах аудиоусилителей. Используя этот пассивный фильтр низких частот, мы можем напрямую снизить высокочастотный шум до уровня небольших помех в стереосистемах.
Фильтр нижних частот как интегратор может использоваться в качестве схем формирования и генерации волн из-за простого преобразования одного типа электрического сигнала в другую форму. Данные фильтры также используются в схемах демодулятора для извлечения требуемых параметров из модулированных сигналов.
В следующей статье мы с вами поговорим о пассивном RC-фильтре высоких частот.
С Уважением, МониторБанк