Пирамидальная сортировка, или как ее еще называют сортировка кучи — один из наиболее эффективных методов сортировки. Этот метод создает кучу из заданного несортированного массива, а затем снова использует эту кучу для сортировки массива.
Сортировка кучи (heapsort) — это метод сортировки, основанный на сравнении, использующий двоичную кучу.
Что такое двоичная куча?
Двоичная куча представляется с использованием полного двоичного дерева. Полное двоичное дерево — это двоичное дерево, в котором все узлы на каждом уровне полностью заполнены, за исключением конечных узлов, а узлы находятся как можно дальше левее.
Двоичная куча — это полное двоичное дерево, в котором элементы или узлы хранятся таким образом, что корневой узел больше, чем два его дочерних узла. Это также называется максимальной кучей.
Элементы в двоичной куче также могут храниться как минимальная куча, в которой корневой узел меньше, чем два его дочерних узла. Мы можем представить кучу в виде двоичного дерева или массива.
При представлении кучи в виде массива, предполагая, что индекс начинается с 0, корневой элемент хранится в 0. В общем случае, если родительский узел находится в позиции I, то левый дочерний узел находится в позиции (2 * I + 1), а правый узел находится в (2 * I + 2).
Общий алгоритм
Ниже приведен общий алгоритм для метода сортировки кучи:
- Создать максимальную кучу из заданных данных таким образом, чтобы корень был самым высоким элементом кучи.
- Удалить корневой узел, то есть самый высокий элемент из кучи, и заменить его последним элементом кучи.
- Затем отрегулировать максимальную кучу, чтобы не нарушать свойства максимальной кучи (heapify).
- Приведенный выше шаг уменьшает размер кучи на 1.
- Повторить вышеуказанные три шага, пока размер кучи не уменьшится до 1.
Как показано в общем алгоритме сортировки данного набора данных в порядке возрастания, мы сначала создаем максимальную кучу для заданных данных.
Давайте рассмотрим пример построения максимальной кучи со следующим набором данных:
6, 10, 2, 4, 1
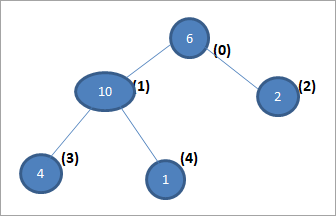
Мы можем построить дерево из этого набора данных следующим образом:
В приведенном выше древовидном представлении, числа в скобках представляют соответствующие позиции в массиве.
Чтобы построить максимальную кучу вышеупомянутого представления, нам нужно выполнить условие кучи, чтобы родительский узел был больше, чем его дочерние узлы. Другими словами, нам нужно “нагромождать” дерево, чтобы преобразовать его в max-heap (максимальную кучу).
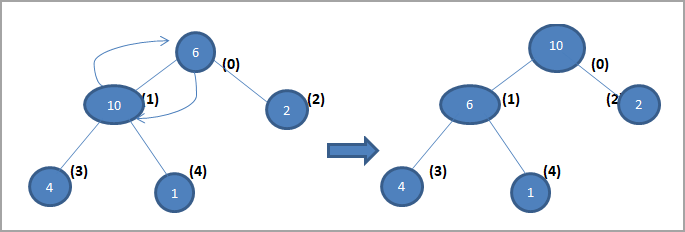
После приведенного выше дерева мы получим максимальную кучу, как показано ниже:
Выше показана максимальная куча, сгенерированная из массива.
Далее мы представим демонстрацию сортировки кучи. Ознакомившись с построением max-heap, мы пропустим подробные шаги по построению max-heap и будем непосредственно показывать максимальную кучу на каждом шаге.
Демонстрация
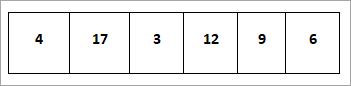
Рассмотрим следующий массив элементов. Нам нужно отсортировать представленный массив, используя метод сортировки кучи:
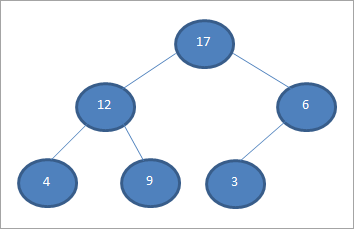
Давайте построим максимальную кучу, как показано ниже, для сортируемого массива:
Как только куча создана, мы представляем ее в виде массива, как показано ниже:
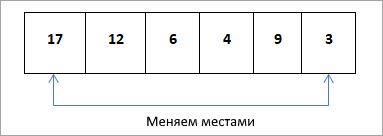
Теперь мы сравниваем 1-й узел (корневой) с последним узлом, а затем меняем их местами. Таким образом, как показано на схеме выше, мы меняем местами 17 и 3 так, чтобы 17 было на последней позиции, а 3 — на первой.
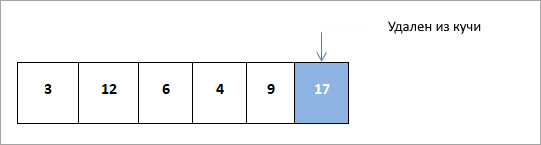
Теперь мы удаляем узел 17 из кучи и помещаем его в отсортированный массив, как показано в заштрихованной части на схеме ниже:
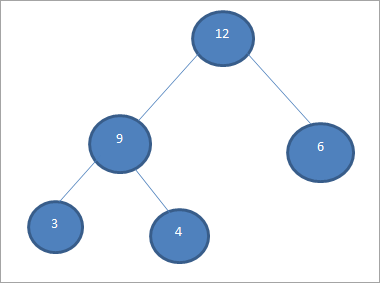
Теперь мы снова создаем кучу для элементов массива. На этот раз размер кучи уменьшен на 1, поскольку мы удалили один элемент (17) из кучи.
Куча оставшихся элементов показана ниже:
На следующем шаге мы повторяем тоже самое.
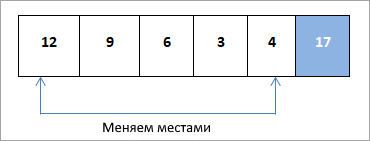
Мы сравниваем и меняем местами корневой элемент и последний элемент в куче:
После замены мы удаляем элемент 12 из кучи и перемещаем его в отсортированный массив:
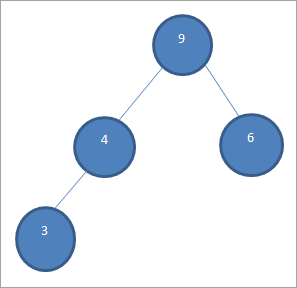
Еще раз мы создаем максимальную кучу для оставшихся элементов, как показано ниже:
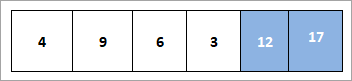
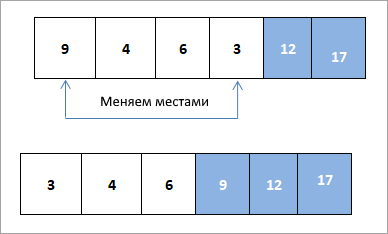
Теперь мы меняем местами корень и последний элемент, т.е. 9 и 3. После замены элемент 9 удаляется из кучи и помещается в отсортированный массив:
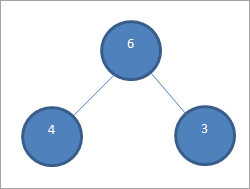
На данный момент у нас есть только три элемента в куче, как показано ниже:
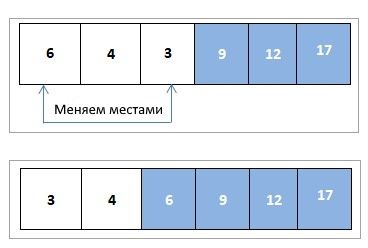
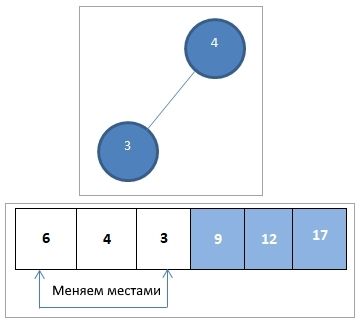
Мы меняем местами 6 и 3 и удаляем элемент 6 из кучи и добавляем его в отсортированный массив:
Теперь мы создаем кучу оставшихся элементов, а затем меняем их местами друг с другом:
После замены 4 и 3 мы удаляем элемент 4 из кучи и добавляем его в отсортированный массив. Теперь у нас остался только один узел в куче, как показано ниже:
Итак, теперь, когда остался только один узел, мы удаляем его из кучи и добавляем в отсортированный массив:
Таким образом, получился показанный выше отсортированный массив, который мы получили в результате сортировки кучи.
На приведенной выше демонстрации мы отсортировали массив в порядке возрастания. Если нам нужно отсортировать массив в порядке убывания, вам нужно выполнить те же шаги, но с минимальной кучей.
Алгоритм данной пирамидальной сортировки идентичен сортировке по выбору, в которой мы выбираем наименьший элемент и помещаем его в отсортированный массив. Однако сортировка кучи выполняется быстрее, чем сортировка по выбору, это касается производительности. Мы можем сказать, что сортировка кучи — это улучшенная версия сортировки по выбору.
Далее мы реализуем пирамидальную сортировку на языках C ++ и Java.
Наиболее важной функцией в обеих реализациях является функция “heapify”. Эта функция вызывается основной процедурой сортировки кучи для перестановки поддерева после удаления узла или при создании максимальной кучи.
Когда мы правильно сложим дерево, то мы сможем получить правильные элементы в их правильных позициях, и, таким образом, массив будет правильно отсортирован.
Ниже приведен код программы на C ++ для реализации сортировки кучи:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
#include <iostream> using namespace std; // функция heapify для нагромождения дерева void heapify(int arr[], int n, int root) { int largest = root; // корень - самый большой элемент int l = 2*root + 1; // слева = 2*корень + 1 int r = 2*root + 2; // справа = 2*корень + 2 // Если левый дочерний элемент больше корневого if (l < n && arr[l] > arr[largest]) largest = l; // Если правый дочерний элемент больше, чем самый большой на данный момент if (r < n && arr[r] > arr[largest]) largest = r; // Если самый большой не является корневым if (largest != root) { //поменять местами корневой и самый большой swap(arr[root], arr[largest]); // Рекурсивное нагромождение поддерева heapify(arr, n, largest); } } // реализация сортировки кучи void heapSort(int arr[], int n) { // создать кучу for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // извлечение элементов из кучи один за другим for (int i=n-1; i>=0; i--) { // Переместить текущий корень в конец swap(arr[0], arr[i]); // снова вызовите max heapify для уменьшенной кучи heapify(arr, i, 0); } } /* печать содержимого массива - служебная функция */ void displayArray(int arr[], int n) { for (int i=0; i<n; ++i) cout << arr[i] << " "; cout << "\n"; } // основная программа int main() { int heap_arr[] = {4,17,3,12,9,6}; int n = sizeof(heap_arr)/sizeof(heap_arr[0]); cout<<"Input array"<<endl; displayArray(heap_arr,n); heapSort(heap_arr, n); cout << "Sorted array"<<endl; displayArray(heap_arr, n); } |
Вывод данных:
| Входной массив 4 17 3 12 9 6 Сортированный массив 3 4 6 9 12 17 |
Далее мы реализуем сортировку кучи на языке Java:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
// Java-программа для реализации сортировки кучи class HeapSort { public void heap_sort(int arr[]) { int n = arr.length; // Создать кучу (переставить массив) for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // Один за другим извлекайте элемент из кучи for (int i=n-1; i>=0; i--) { // Переместить текущий корень в конец int temp = arr[0]; arr[0] = arr[i]; arr[i] = temp; // вызов max heapify для уменьшенной кучи heapify(arr, i, 0); } } // нагромождение поддерева void heapify(int arr[], int n, int root) { int largest = root; // Инициализируйте его как корневой int l = 2*root + 1; // слева = 2*корень + 1 int r = 2*root + 2; // справа = 2*корень + 2 // Если левый дочерний элемент больше корневого if (l < n && arr[l] > arr[largest]) largest = l; // Если правый дочерний элемент больше, чем самый большой на данный момент if (r < n && arr[r] > arr[largest]) largest = r; // Если самый большой не является корневым if (largest != root) { int swap = arr[root]; arr[root] = arr[largest]; arr[largest] = swap; // Рекурсивно нагромождать затронутое поддерево heapify(arr, n, largest); } } //печать содержимого массива - служебная функция static void displayArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } } class Main{ // основная программа public static void main(String args[]) { int arr[] = {4,17,3,12,9,6}; int n = arr.length; HeapSort ob = new HeapSort(); System.out.println("Input array: "); HeapSort.displayArray(arr); ob.heap_sort(arr); System.out.println("Sorted array:"); HeapSort.displayArray(arr); } } |
Вывод данных:
| Входной массив: 4 17 3 12 9 6 Сортированный массив: 3 4 6 9 12 17 |
Итог
Пирамидальная сортировка или сортировка кучи — это метод сортировки на основе сравнения с использованием двоичной кучи.
Этот метод можно назвать улучшением метода сортировки по выбору, поскольку оба этих метода сортировки работают с аналогичной логикой многократного поиска самого большого или самого маленького элемента в массиве и последующего помещения его в отсортированный массив.
Сортировка кучи использует max-heap или min-heap для сортировки массива. Первым шагом в сортировке кучи является создание минимальной или максимальной кучи из данных массива, а затем рекурсивное удаление корневого элемента и увеличение кучи до тех пор, пока в куче не останется только один узел.
Сортировка кучи — эффективный алгоритм, и он выполняется быстрее, чем сортировка по выбору. Он может использоваться для сортировки почти отсортированного массива или поиска k самых больших или самых маленьких элементов в массиве.
В этой статье мы завершили темы о методах сортировки в C ++. В нашей следующей статье мы начнем изучение связного списка в C ++.
С Уважением, МониторБанк