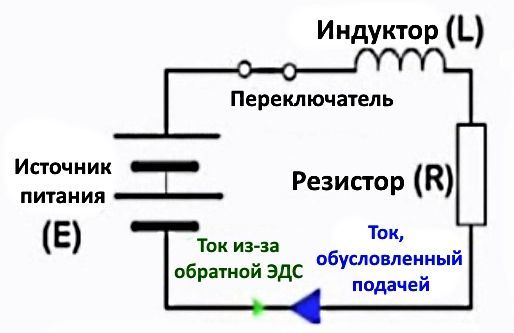
 Когда ток подается на индуктор, требуется некоторое время, чтобы ток достиг своего максимального значения, после чего он останется в «устойчивом состоянии», пока какое-либо другое событие не вызовет изменение входа.
Когда ток подается на индуктор, требуется некоторое время, чтобы ток достиг своего максимального значения, после чего он останется в «устойчивом состоянии», пока какое-либо другое событие не вызовет изменение входа.
| Серия статей по переходным процессам в цепях постоянного тока |
Время, необходимое для того, чтобы ток нарастал до установившегося значения в цепи LR, зависит от:
• Сопротивления (R)
Это полное сопротивление цепи, которое включает в себя сопротивление постоянному току самой катушки индуктивности (RL) плюс любое внешнее сопротивление цепи.
• Индуктивности L
Который пропорционален квадрату числа витков, площади поперечного сечения катушки и проницаемости сердечника.
Индуктор противостоит изменениям в текущем потоке
Когда схема включена (картинка ниже), ток быстро меняется от нуля, это внезапное изменение создает быстро расширяющееся магнитное поле вокруг катушек индуктивности и при этом индуцирует напряжение обратно в катушку. Это индуцированное напряжение (называемое обратной ЭДС) создает ток (зеленая стрелка на принципиальной схеме), текущий в противоположном направлении по отношению к исходному току (синяя стрелка на принципиальной схеме), подаваемому батареей.
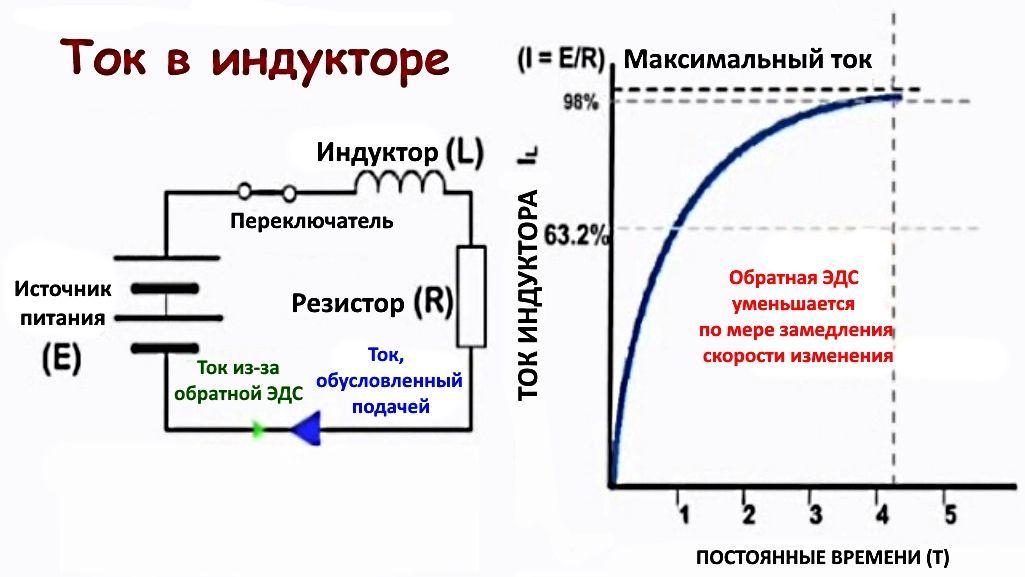
Результатом внезапного изменения напряжения при включении цепи является то, что скорость изменения тока цепи от 0 В до максимального тока увеличивается медленнее, чем в полностью резистивной цепи. Если бы начальная скорость изменения тока в цепи LR продолжалась линейно, ток достиг бы своего максимального или устойчивого «значения состояния» за время (T), определяемое как:
T = L/R секунд
T — является постоянной времени и измеряется в секундах.
L — это индуктивность, измеряемая в Генри.
R — общее сопротивление в цепи, измеряется в Омах.
Секунды и Генри обычно слишком велики для большинства измерений в электронике, и обычно используются милли- и микроединицы, но не забывайте при расчетах преобразовывать любую из этих единиц в секунды или Генри для использования в формулах.
Однако увеличение тока не является линейным, а следует изогнутой «экспоненциальной» траектории, и за одну постоянную времени (обозначенную на картинке выше вертикальной пунктирной линией) ток (обозначенный горизонтальной пунктирной линией) возрастет только до 63,2% от его максимального (установившегося) значения. После двух постоянных времени он достигнет 86,5%, после 3 постоянных времени 95% и так далее, пока не достигнет 99,5%, что считается его максимальным значением после 5 постоянных времени.
Разряд
Если цепь отключена, ток не сразу падает до нуля, он снова падает экспоненциально, и через один период постоянной времени достигнет 36,8% от предыдущего значения устойчивого состояния (т.е. значение устойчивого состояния -63,2%). Считается, что он достигает нуля за пять периодов постоянной времени.
Экспоненциальная кривая
Изменение тока в индукторе в ответ на ступенчатое изменение входного сигнала является экспоненциальным. В течение ряда равных периодов времени ток заряжает индуктор до его максимального значения на процент от оставшейся разницы между текущим и максимальным значениями. Таким образом, хотя эта разница продолжает сокращаться, дополнительный заряд, накопленный в течение каждого периода времени, также уменьшается. Результатом этого является то, что ток никогда не сможет достичь максимума!
Почему 63,2%?
Если ток никогда не достигает своего установившегося значения, возникает проблема измерения времени, необходимого для полного заряда. Вот почему используется идея постоянной времени (время, необходимое для заряда на 63,2%). Зачем выбирать 63,2%, когда есть более простые цифры, такие как 50%, которые можно было бы использовать? Ну, 50% было бы неплохо, но создало бы неудобную формулу для расчета затраченного времени.
Все просто!
Так получилось, что использование 63,2% (что не слишком отличается от 50%) приводит к хорошей простой формуле L/R для постоянной времени индуктора и CR для постоянной времени конденсатора. Это значительно упрощает вычисления, и поскольку ток достигнет 99,5% от установившегося значения через 5 постоянных времени, на практике этого достаточно, чтобы считать, что достигнуто максимальное значение.
Для закрепления изученного материала пройдите наш тест.
С Уважением, МониторБанк