Пузырьковая сортировка — самый простой из методов сортировки.
Пузырьковая сортировка — самый простой из методов сортировки.
В методе пузырьковой сортировки каждый элемент списка сравнивается с соседним элементом. Таким образом, если в списке A n элементов, то A[0] сравнивается с A[1], A[1] сравнивается с A[2] и так далее.
После сравнения, если первый элемент больше второго, два элемента меняются местами.
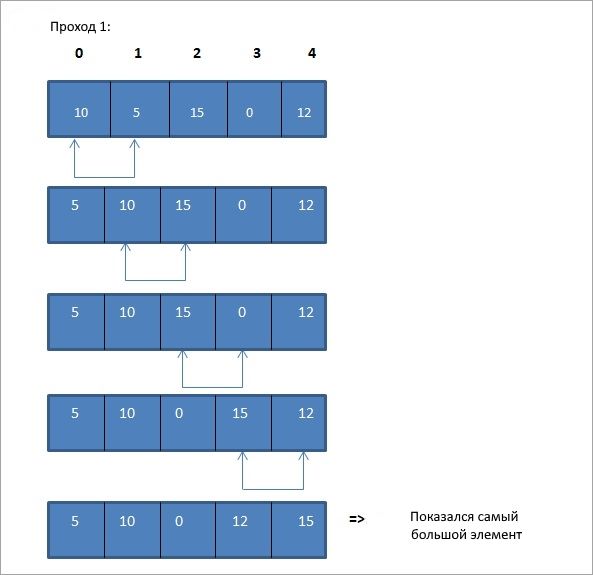
При использовании метода пузырьковой сортировки, сортировка выполняется за проходы или итерации. Таким образом, в конце каждой итерации самый большой элемент помещается на свое место в списке. Другими словами, самый большой элемент в списке всплывает.
Ниже мы привели общий алгоритм метода пузырьковой сортировки:
Шаг 1 : Для i = 0 до N-1 запускаем шаг 2
Шаг 2 : Для J = i + 1 до N – повторяем
Шаг 3 : Если A[J] > A[i]
Меняем местами A[J] и A[i ]
[Конец внутреннего цикла for]
[Конец внешнего цикла for]
Шаг 4 : Выход
Вот псевдокод алгоритма пузырьковой сортировки, в котором мы проходим по списку, используя два итеративных цикла.
В первом цикле мы начинаем с 0 -го элемента, а в следующем цикле начинаем с соседнего элемента. В теле внутреннего цикла мы сравниваем каждый из соседних элементов и меняем их местами, если они не в нужном месте. В конце каждой итерации внешнего цикла самый тяжелый элемент всплывает в конце.
Псевдокод:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Процедура пузырьковой сортировки (array , N) array — список элементов для сортировки N — размер массива начало обмен = ложь повторение для I = 1 до N-1 , если array[i-1] > array[i], тогда меняем массив[i] -1] и массив[i] поменялись местами = правда конец, если конец до тех пор, пока не будет заменена завершение процедуры |
Выше приведен псевдокод для метода пузырьковой сортировки. Давайте теперь проиллюстрируем эту технику, используя подробные схемы.
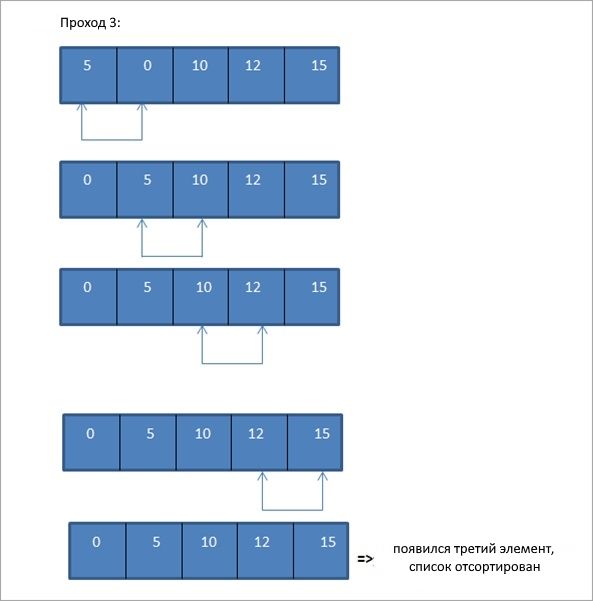
Массив полностью отсортирован.
Приведенные выше схемы можно обобщить в табличной форме, как показано ниже:
| Проход | Несортированый список | Сравнение | Отсортированный список |
| 1 | {10,5,15,0,12} | {10,5} | {5,10,15,0,12} |
| {5,10,15,0,12} | {10,15} | {5,10,15,0,12} | |
| {5,10,15,0,12} | {15,0} | {5,10,0,15,12} | |
| {5,10,0,15,12} | {15,12} | {5,10,0,12,15} | |
| 2 | {5,10,0,12,15} | {5,10} | {5,10,0,12,15} |
| {5,10,0,12,15} | {10,0} | {5,0,10,12,15} | |
| {5,0,10,12,15} | {10,12} | {5,0,10,12,15} | |
| 3 | {5,0,10,12,15} | {5,0} | {0,5,10,12,15} |
| {5,0,10,12,15} | {5,10} | {5,0,10,12,15} | |
| {5,0,10,12,15} | СОРТИРОВКА | ||
Как показано на схемах, при каждом проходе самый большой элемент всплывает до последнего, тем самым сортируя список при каждом проходе. Как упоминалось во введении, каждый элемент сравнивается с соседним элементом и заменяется другим, если они не в нужном месте.
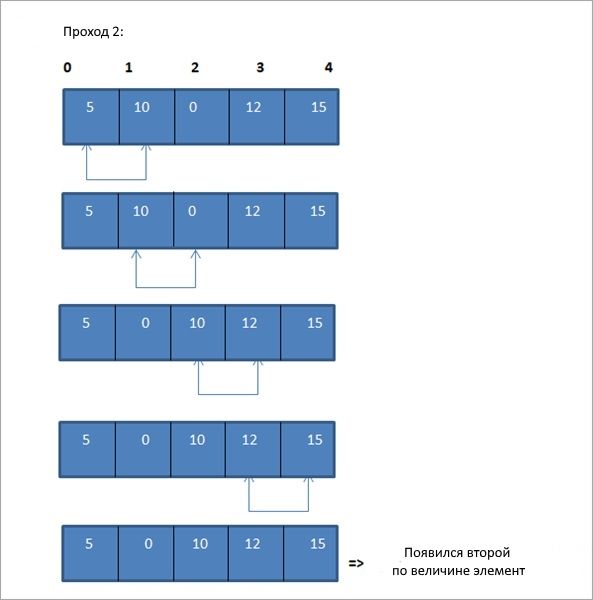
Таким образом, как показано на схемах, в конце первого прохода, если массив должен быть отсортирован в порядке возрастания, самый большой элемент помещается в конец списка. При втором проходе второй по величине элемент помещается в предпоследнюю позицию в списке и так далее.
Когда мы достигнем N-1 (где N — общее количество элементов в списке) проходов, весь список будет отсортирован.
Метод пузырьковой сортировки может быть реализован на любом языке программирования. Ниже мы реализовали алгоритм пузырьковой сортировки с использованием языков C++ и Java.
Давайте посмотрим пример пузырьковой сортировки на языке C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
#include<iostream> using namespace std; int main () { int i, j,temp,pass=0; int a[10] = {10,2,0,14,43,25,18,1,5,45}; cout <<"Input list ...\n"; for(i = 0; i<10; i++) { cout <<a[i]<<"\t"; } cout<<endl; for(i = 0; i<10; i++) { for(j = i+1; j<10; j++) { if(a[j] < a[i]) { temp = a[i]; a[i] = a[j]; a[j] = temp; } } pass++; } cout <<"Sorted Element List ...\n"; for(i = 0; i<10; i++) { cout <<a[i]<<"\t"; } cout<<"\nNumber of passes taken to sort the list:"<<pass<<endl; return 0; } |
Вывод данных:
| Список ввода… 10 2 0 14 43 25 18 1 5 45 Отсортированный список элементов… 0 1 2 5 10 14 18 25 43 45 Количество проходов для сортировки списка: 10 |
Теперь, давайте посмотрим пример пузырьковой сортировки на языке Java:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
class Main { public static void main(String[] args) { int pass = 0; int[] a = {10,-2,0,14,43,25,18,1,5,45}; System.out.println("Input List..."); for(int i=0;i<10;i++) { System.out.print(a[i] + " "); } for(int i=0;i<10;i++) { for (int j=0;j<10;j++) { if(a[i]<a[j]) { int temp = a[i]; a[i]=a[j]; a[j] = temp; } } pass++; } System.out.println("\nSorted List ..."); for(int i=0;i<10;i++) { System.out.print(a[i] + " "); } System.out.println("\nNumber of passes taken to complete sort:" + pass); } } |
Вывод данных:
| Список входных данных… 10 -2 0 14 43 25 18 1 5 45 Отсортированный список -2 0 1 5 10 14 18 25 43 45 Количество проходов, необходимых для завершения сортировки:10 |
В обеих программах мы использовали массив из 10 элементов и сортировали его с помощью техники пузырьковой сортировки. В обеих программах мы использовали два цикла for для перебора соседних элементов массива.
В конце каждого прохода (внешний цикл) самый большой элемент массива всплывает до конца массива. Мы также подсчитали количество проходов, необходимых для сортировки всего массива.
Анализ сложности алгоритма пузырьковой сортировки
Из псевдокода и схем, которые мы представили выше, в пузырьковой сортировке мы делаем N-1 сравнений на первом проходе, N-2 сравнений на втором проходе и так далее.
Следовательно, общее количество сравнений в пузырьковой сортировке равно:
Сумма = (N-1) + (N-2) + (N-3)+ … + 3 + 2 + 1
= N(N-1)/2
= O(n2) => временная сложность метода пузырьковой сортировки
Таким образом, различные сложности метода пузырьковой сортировки приведены ниже:
| Временная сложность в худшем случае | O(n 2) |
| Временная сложность в лучшем случае | O(n) |
| Средняя временная сложность | O(n 2) |
| Пространственная сложность | O(1) |
Метод пузырьковой сортировки требует только одного дополнительного места в памяти для временной переменной для облегчения замены. Следовательно, пространственная сложность алгоритма пузырьковой сортировки составляет O (1).
Обратите внимание, что наилучшая временная сложность для метода пузырьковой сортировки будет, когда список уже отсортирован, и это будет O (n).
Итог
Основным преимуществом пузырьковой сортировки является простота алгоритма. При пузырьковой сортировке, при каждом проходе, самый большой элемент всплывает до конца списка, если массив отсортирован в порядке возрастания.
Точно так же для сортировки списка в порядке убывания наименьший элемент будет находиться на нужном месте в конце каждого прохода.
Являясь самым простым и легким в реализации методом сортировки, пузырьковая сортировка обычно используется для ознакомления пользователей с сортировкой. Пузырьковая сортировка также применяется в компьютерной графике, где нужно заполнение краев многоугольника и т. д. Такое применение требует пузырьковой сортировки для сортировки вершин, выстилающих многоугольник.
В нашей следующей статье мы подробно поговорим о сортировке выбором в C++.
С Уважением, МониторБанк