Сортировку Шелла часто называют улучшенным вариантом сортировки вставками. Если помните, то при сортировке вставками мы увеличиваем число на 1, чтобы сравнить элементы и поместить их в нужное место.
При сортировке Шелла список сортируется путем разбиения его на несколько меньших подсписков. Не обязательно, чтобы списки были с непрерывными элементами. Вместо этого метод сортировки Шелла использует приращение i, которое также называется «промежутком», и использует его для создания списка элементов, которые находятся на расстоянии «i» друг от друга.
Общий алгоритм
Общий алгоритм сортировки Шелла приведен ниже:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
shell_sort (A, N) where A – list to be sorted; N – gap_size set gap_size = N, flag = 1 while gap_size > 1 or flag = 1, repeat begin set flag = 0 set gap_size = (gap_size + 1)/2 end for i = 0 to i< (N-gap_size) repeat begin if A[i + gap_size] > A[i] swap A[i + gap_size], A[i] set flag = 0 end end |
Таким образом, в приведенном выше алгоритме мы сначала устанавливаем N, который является промежутком для сортировки массива A, с использованием сортировки Шелла. На следующем шаге мы разделяем массив на подмассивы, с помощью пробела. Затем на следующем шаге мы сортируем каждый из подмассивов, чтобы в конце цикла мы получили отсортированный массив.
Далее давайте рассмотрим подробный пример, чтобы лучше понять сортировку Шелла, с помощью графического представления.
Демонстрация
Давайте рассмотрим сортировку Шелла на примере.
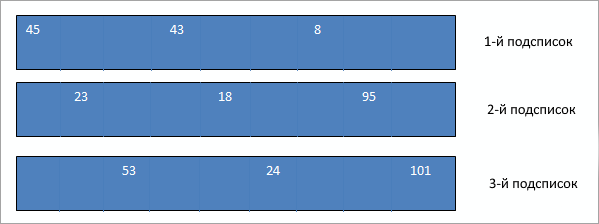
Рассмотрим следующий массив из 10 элементов:
Если мы обеспечим разрыв в 3, то у нас будут следующие вложенные списки с каждым элементом, который находится на расстоянии 3 элементов друг от друга. Затем мы сортируем эти три подсписка:
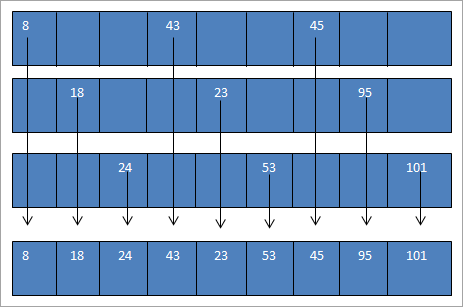
Отсортированные вложенные списки и результирующий список, который мы получаем после объединения трех отсортированных вложенных списков, показаны ниже:
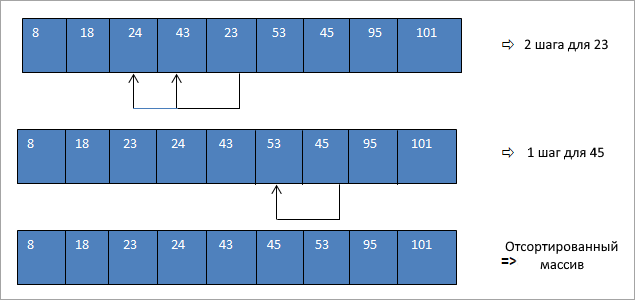
Приведенный выше массив, который мы получили после объединения отсортированных подмассивов, почти отсортирован. Теперь мы можем выполнить сортировку вставкой в этот список и отсортировать весь массив. Этот последний шаг показан ниже:
Как видно выше, после выполнения сортировки Шелла и объединения отсортированных подсписков нам потребовалось всего три шага, чтобы полностью отсортировать список. Таким образом, становится видно, что можем значительно сократить количество шагов, необходимых для сортировки массива.
Выбор приращения для создания вложенных списков является уникальной особенностью сортировки Шелла.
Давайте посмотрим на реализацию сортировки Шелла в C ++ ниже:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
#include <iostream> using namespace std; // реализация сортировки Шелла int shellSort(int arr[], int N) { for (int gap = N/2; gap > 0; gap /= 2) { for (int i = gap; i < N; i += 1) { //сортировка подсписков, созданных с помощью gap int temp = arr[i]; int j; for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) arr[j] = arr[j - gap]; arr[j] = temp; } } return 0; } int main() { int arr[] = {45,23,53,43,18,24,8,95,101}, i; //Вычислить размер массива int N = sizeof(arr)/sizeof(arr[0]); cout << "Array to be sorted: \n"; for (int i=0; i<N; i++) cout << arr[i] << " "; shellSort(arr, N); cout << "\nArray after shell sort: \n"; for (int i=0; i<N; i++) cout << arr[i] << " "; return 0; } |
Вывод данных:
| Массив, подлежащий сортировке: 45 23 53 43 18 24 8 95 101 Массив после сортировки Шелла: 8 18 23 24 43 45 53 95 101 |
Мы использовали тот же список, что и на демонстрации, и теперь стало видно, что сначала мы создаем два вложенных списка, а затем еще больше сокращаем разрыв. Как только вложенные списки созданы в соответствии с указанным пробелом, мы сортируем каждый из вложенных списков. После того, как все вложенные списки отсортированы, мы получаем почти отсортированный список. Теперь этот список можно отсортировать с помощью базовой сортировки вставкой, которая займет очень мало ходов.
Далее давайте реализуем сортировку Шелла с использованием языка Java:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
// Java-класс для сортировки Шелла class ShellSort { //функция для сортировки массива с помощью сортировки Шелла int sort(int arr[]) { int N = arr.length; // Начните с большого разрыва, затем сократите разрыв for (int gap = N/2; gap > 0; gap /= 2) { //сортировка подсписков, созданных с помощью gap for (int i = gap; i < N; i += 1) { int temp = arr[i]; int j; for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) arr[j] = arr[j - gap]; arr[j] = temp; } } return 0; } } class Main{ public static void main(String args[]) { int arr[] = {45,23,53,43,18,24,8,95,101}; int N = arr.length; System.out.println("Array to be sorted: "); for (int i=0; i<N; ++i) System.out.print(arr[i] + " "); System.out.println(); ShellSort ob = new ShellSort(); ob.sort(arr); System.out.println(""Array after shell sort: "); for (int i=0; i<N; ++i) System.out.print(arr[i] + " "); System.out.println(); } } |
Вывод данных:
| Массив для сортировки: 45 23 53 43 18 24 8 95 101 Массив после сортировки Шелла: 8 18 23 24 43 45 53 95 101 |
Мы реализовали одну и ту же логику для сортировки Шелла как в программе на C ++, так и в Java. Таким образом, как объяснено выше в программе Java, мы сначала делим массив на подмассивы, а затем сортируем их, чтобы получить полный отсортированный массив.
Итог
Сортировка Шелла — это высокоэффективный алгоритм, который работает намного эффективнее, чем сортировка вставками.
В то время как сортировка вставками выполняется путем увеличения ее элементов на 1, сортировка Шелла использует параметр “gap” для разделения массива на подмассивы, элементы которых разделены на “промежутки”. Затем мы можем отсортировать отдельный список, используя сортировку вставками, чтобы получить полный отсортированный массив.
Сортировка Шелла выполняется быстрее, чем сортировка вставками, и для сортировки массива требуется меньше ходов по сравнению с сортировкой вставками.
В нашей следующей статье будет рассмотрен метод пирамидальной сортировки, или как ее еще называют сортировки кучи, для сортировки структуры данных.
С Уважением, МониторБанк