Структура данных стека в C++

Структура данных стека Стек — это фундаментальная структура данных, которая используется для хранения элементов линейным способом.

Стек следует LIFO (последний вход, первый выход) порядок или подход, в котором выполняются операции. Это означает, что элемент, который был добавлен последним в стек, будет первым элементом, который будет удален из стека.

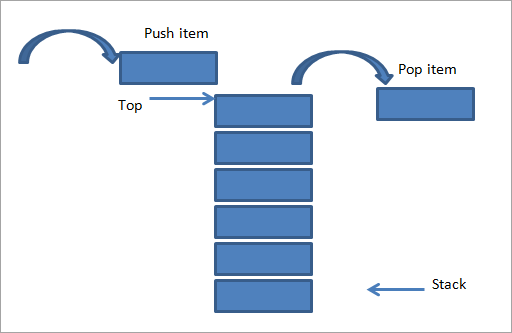
Ниже приведена схема стека:

Как показано выше, есть куча элементов, уложенных друг на друга. Если мы хотим добавить к ним еще один элемент, то мы добавляем его в верхнюю часть стека, как показано на рисунке выше (слева). Эта операция добавления элемента в стек называется “Push”.

В правой части мы показали противоположную операцию, то есть мы удаляем элемент из стека. Это также делается с того же конца, то есть с вершины стека. Эта операция называется “Pop”.

Как показано на рисунке выше, мы видим, что push и pop выполняются с одного конца. Это заставляет стек следовать порядку LIFO. Позиция или конец, из которого элементы вставляются или извлекаются в / из стека, называется “Вершиной стека”.

Изначально, когда в стеке нет элементов, верх стека устанавливается равным -1. Когда мы добавляем элемент в стек, верхняя часть стека увеличивается на 1, указывая, что элемент добавлен. Верхняя часть стека уменьшается на 1, когда элемент извлекается из стека.

Далее мы покажем некоторые из основных операций структуры данных стека, которые нам потребуются при реализации стека.

Основные операции

Ниже приведены основные операции, которые поддерживаются стеком.

push – добавляет или помещает элемент в стек.
pop – удаляет или выталкивает элемент из стека.
peek – возвращает верхний элемент стека, но не удаляет его.
isFull – проверяет, заполнен ли стек.
isEmpty – проверяет, пуст ли стек.

Демонстрация

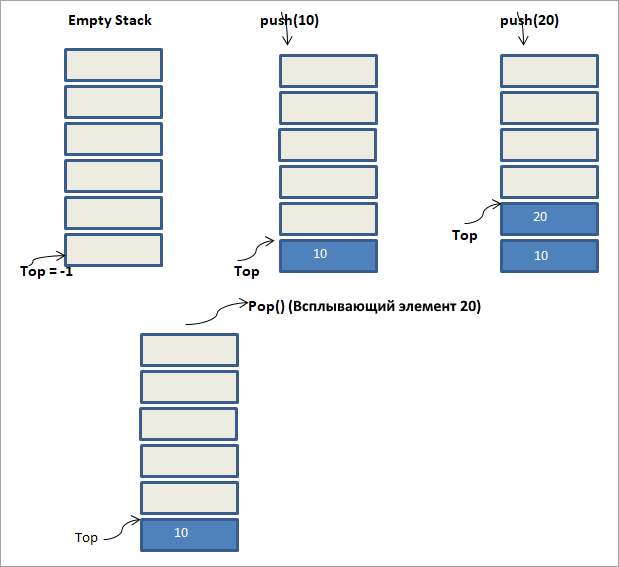
На приведенном выше рисунке показана последовательность операций, которые выполняются в стеке. Изначально стек пуст. Для пустого стека верх стека устанавливается равным -1.

Далее мы помещаем элемент 10 в стек. Видно, что вершина стека теперь указывает на элемент 10.

Читать также: Структура данных очереди в C++

Далее мы выполняем еще одну операцию push с элементом 20, в результате чего вершина стека теперь указывает на 20. Это состояние показывает третий рисунок.

Теперь на последнем рисунке мы выполняем операцию pop (). В результате операции pop элемент, указанный в верхней части стека, удаляется из стека. Следовательно, на рисунке мы видим, что элемент 20 удален из стека. Таким образом, вершина стека теперь указывает на 10.

Реализация

1) Использование массивов

Ниже приведена реализация стека на C ++ с использованием массивов:

#include<iostream>
using namespace std;
  
#define MAX 1000 //максимальный размер стека
  
class Stack
{
   int top;
   public:
   int myStack[MAX]; //массив стека
  
   Stack() { top = -1; }
   bool push(int x);
   int pop();
   bool isEmpty();
};
   //помещает элемент в стек
   bool Stack::push(int item)
   {
      if (top >= (MAX-1)) {
      cout << "Stack Overflow!!!";
      return false;
   }
else {
   myStack[++top] = item;
   cout<<item<<endl;
   return true;
   }
}
  
//удаляет или выталкивает элементы из стека
int Stack::pop()
{
   if (top < 0) {
      cout << "Stack Underflow!!";
      return 0;
   }
else {
       int item = myStack[top--];
      return item;
   }
}
  
//проверьте, пуст ли стек
bool Stack::isEmpty()
{
   return (top < 0);
}
  
// основная программа для демонстрации функций стека
int main()
{
   class Stack stack;
   cout<<"The Stack Push "<<endl;
   stack.push(2);
   stack.push(4);
   stack.push(6);
   cout<<"The Stack Pop : "<<endl;
   while(!stack.isEmpty())
      {
      cout<<stack.pop()<<endl;
      }
   return 0;
}

#include<iostream>

using namespace std;

#define MAX 1000 //максимальный размер стека

class Stack

{

int top;

public:

int myStack[MAX]; //массив стека

Stack() { top = -1; }

bool push(int x);

int pop();

bool isEmpty();

};

//помещает элемент в стек

bool Stack::push(int item)

{

if (top >= (MAX-1)) {

cout << "Stack Overflow!!!";

return false;

}

else {

myStack[++top] = item;

cout<<item<<endl;

return true;

}

//удаляет или выталкивает элементы из стека

int Stack::pop()

{

if (top < 0) {

cout << "Stack Underflow!!";

return 0;

}

else {

int item = myStack[top--];

return item;

}

//проверьте, пуст ли стек

bool Stack::isEmpty()

{

return (top < 0);

}

// основная программа для демонстрации функций стека

int main()

{

class Stack stack;

cout<<"The Stack Push "<<endl;

stack.push(2);

stack.push(4);

stack.push(6);

cout<<"The Stack Pop : "<<endl;

while(!stack.isEmpty())

{

cout<<stack.pop()<<endl;

}

return 0;

}

Вывод данных:

The Stack Push
2
4
6
The Stack Pop:
6
4
2

В выводных данных мы можем видеть, что элементы помещаются в стек в одном порядке и извлекаются из стека в обратном порядке. Это демонстрирует подход LIFO (последний вход, первый выход) для стека.

Для приведенной выше реализации стека в виде массива мы можем сделать вывод, что это очень легко реализовать, поскольку указатели не задействованы. Но в то же время размер стека статичен, и стек не может расти или уменьшаться динамически.

Далее мы реализуем стек с использованием массивов на языке программирования Java:

class Stack
{
   static final int MAX = 1000; // Максимальный размер стека
   int top;
   int myStack[] = new int[MAX];
  
   boolean isEmpty()
   {
      return (top < 0);
   }
   Stack() {
      top = -1;
   }
  
   boolean push(int item)
   {
      if (top >= (MAX-1))
      {
         System.out.println("Stack Overflow");
         return false;
      }
   else
   {
   myStack[++top] = item;
   System.out.println(item);
   return true;
   }
}
  
int pop()
   {
      if (top < 0)
      {
         System.out.println("Stack Underflow");
         return 0;
      }
else
      {
         int item = myStack[top--];
         return item;
      }
   }
}
//Основной код класса
class Main
{
   public static void main(String args[])
   {
      Stack stack = new Stack();
      System.out.println("Stack Push:");
      stack.push(1);
      stack.push(3);
      stack.push(5);
      System.out.println("Stack Pop:");
      while(!stack.isEmpty())
      {
         System.out.println(stack.pop());
      }
   }
}

class Stack

{

static final int MAX = 1000; // Максимальный размер стека

int top;

int myStack[] = new int[MAX];

boolean isEmpty()

{

return (top < 0);

}

Stack() {

top = -1;

}

boolean push(int item)

{

if (top >= (MAX-1))

{

System.out.println("Stack Overflow");

return false;

}

else

{

myStack[++top] = item;

System.out.println(item);

return true;

}

int pop()

{

if (top < 0)

{

System.out.println("Stack Underflow");

return 0;

}

else

{

int item = myStack[top--];

return item;

}

//Основной код класса

class Main

{

public static void main(String args[])

{

Stack stack = new Stack();

System.out.println("Stack Push:");

stack.push(1);

stack.push(3);

stack.push(5);

System.out.println("Stack Pop:");

while(!stack.isEmpty())

{

System.out.println(stack.pop());

}

Вывод данных:

Stack Push:
1
3
5
Stack Pop:
5
3
1

Логика реализации такая же, как и в реализации на C ++. На выходе показана методика LIFO по вводу и извлечению элементов в / из стека.

Как уже говорилось, реализация стека с использованием массивов является самой простой реализацией, но носит статический характер, поскольку мы не можем динамически увеличивать или уменьшать стек.

2) Использование связного списка

Далее мы реализуем операции стека с использованием связного списка как в C++, так и в Java. Сначала мы продемонстрируем реализацию на C++:

#include <iostream>
using namespace std;
  
// класс для представления узла стека
class StackNode {
   public:
   int data;
   StackNode* next;
   };
  
StackNode* newNode(int data) {
   StackNode* stackNode = new StackNode();
   stackNode->data = data;
   stackNode->next = NULL;
   return stackNode;
   }
  
int isEmpty(StackNode *root) {
   return !root;
   }
  
void push(StackNode** root, int new_data){
   StackNode* stackNode = newNode(new_data);
   stackNode->next = *root;
   *root = stackNode;
   cout<<new_data<<endl;
   }
  
int pop(StackNode** root){
   if (isEmpty(*root))
   return -1;
   StackNode* temp = *root;
   *root = (*root)->next;
   int popped = temp->data;
   free(temp);
  
   return popped;
}
int peek(StackNode* root)
{
   if (isEmpty(root))
   return -1;
   return root->data;
}
  
int main()
{
   StackNode* root = NULL;
   cout<<"Stack Push:"<<endl;
   push(&root, 100);
   push(&root, 200);
   push(&root, 300);
   cout<<"\nTop element is "<<peek(root)<<endl;
   cout<<"\nStack Pop:"<<endl;
   while(!isEmpty(root)){
   cout<<pop(&root)<<endl;
}
  
cout<<"Top element is "<<peek(root)<<endl;
  
return 0;
}

#include <iostream>

using namespace std;

// класс для представления узла стека

class StackNode {

public:

int data;

StackNode* next;

};

StackNode* newNode(int data) {

StackNode* stackNode = new StackNode();

stackNode->data = data;

stackNode->next = NULL;

return stackNode;

}

int isEmpty(StackNode *root) {

return !root;

}

void push(StackNode** root, int new_data){

StackNode* stackNode = newNode(new_data);

stackNode->next = *root;

*root = stackNode;

cout<<new_data<<endl;

}

int pop(StackNode** root){

if (isEmpty(*root))

return -1;

StackNode* temp = *root;

*root = (*root)->next;

int popped = temp->data;

free(temp);

return popped;

}

int peek(StackNode* root)

{

if (isEmpty(root))

return -1;

return root->data;

}

int main()

{

StackNode* root = NULL;

cout<<"Stack Push:"<<endl;

push(&root, 100);

push(&root, 200);

push(&root, 300);

cout<<"\nTop element is "<<peek(root)<<endl;

cout<<"\nStack Pop:"<<endl;

while(!isEmpty(root)){

cout<<pop(&root)<<endl;

}

cout<<"Top element is "<<peek(root)<<endl;

return 0;

}

Вывод данных:

Stack Push:
100
200
300
Top element is 300
Stack Pop:
300
200
100
Top element is -1

Далее мы представим реализацию стека на Java с использованием связного списка:

class LinkedListStack {
  
   StackNode root;
  
   static class StackNode {
      int data;
      StackNode next;
  
      StackNode(int data) {
         this.data = data;
      }
   }
  
   public boolean isEmpty() {
      if (root == null) {
         return true;
      } else return false;
  }
  
public void push(int new_data) {
   StackNode newNode = new StackNode(new_data);
  
   if (root == null) {
      root = newNode;
      } else {
         StackNode temp = root;
         root = newNode;
         newNode.next = temp;
      }
   System.out.println(new_data);
}
  
public int pop() {
   int popped = Integer.MIN_VALUE;
   if (root == null) {
   System.out.println("Stack is Empty");
   } else {
      popped = root.data;
      root = root.next;
   }
return popped;
}
public int peek() {
   if (root == null) {
      System.out.println("Stack is empty");
      return Integer.MIN_VALUE;
      } else {
         return root.data;
         }
         
      }
}
class Main{
public static void main(String[] args) {
  
   LinkedListStack stack = new LinkedListStack();
   System.out.println("Stack Push:");
   stack.push(100);
   stack.push(200);
   stack.push(300);
   System.out.println("Top element is " + stack.peek());
  
   System.out.println("Stack Pop:");
   while(!stack.isEmpty()){
   System.out.println(stack.pop());
   }
System.out.println("Top element is " + stack.peek());
}
}

class LinkedListStack {

StackNode root;

static class StackNode {

int data;

StackNode next;

StackNode(int data) {

this.data = data;

}

public boolean isEmpty() {

if (root == null) {

return true;

} else return false;

}

public void push(int new_data) {

StackNode newNode = new StackNode(new_data);

if (root == null) {

root = newNode;

} else {

StackNode temp = root;

root = newNode;

newNode.next = temp;

}

System.out.println(new_data);

}

public int pop() {

int popped = Integer.MIN_VALUE;

if (root == null) {

System.out.println("Stack is Empty");

} else {

popped = root.data;

root = root.next;

}

return popped;

}

public int peek() {

if (root == null) {

System.out.println("Stack is empty");

return Integer.MIN_VALUE;

} else {

return root.data;

}

class Main{

public static void main(String[] args) {

LinkedListStack stack = new LinkedListStack();

System.out.println("Stack Push:");

stack.push(100);

stack.push(200);

stack.push(300);

System.out.println("Top element is " + stack.peek());

System.out.println("Stack Pop:");

while(!stack.isEmpty()){

System.out.println(stack.pop());

}

System.out.println("Top element is " + stack.peek());

}

Вывод данных:

Stack Push:
100
200
300
Top element is 300
Stack Pop:
300
200
100
Stack is empty
Top element is -2147483648

Читать также: Полиморфизм в С++

Мы только что показали реализации программ на C++ и Java для стека с использованием связных списков. Мы представили каждую запись стека как узел связного списка. Наиболее важным преимуществом этой реализации является то, что она динамична. Это означает, что мы можем увеличивать или уменьшать размер стека в соответствии с нашими требованиями.

Это не похоже на случай реализации стека с использованием массивов, в которых мы должны заранее объявлять размер и не можем изменять его динамически.

Недостатком этой реализации является то, что, поскольку мы используем указатели повсюду, это занимает слишком много места по сравнению с реализацией массива.

Применения стека

Давайте обсудим некоторые применения структуры данных стека. Структура данных стека используется в ряде приложений в программировании, в основном из-за ее простоты реализации.

Ниже мы кратко опишем некоторые применения стека:

1) Инфикс в постфиксные выражения

Любое общее арифметическое выражение имеет вид operand1 OP operand2 .

Основываясь на позиции оператора OP, мы имеем следующие типы выражений:

Инфикс – общая форма инфиксного выражения — “operand1 OP operand2”. Это базовая форма выражения, которую мы постоянно используем в математике.
Префикс – когда оператор помещается перед операндами, это префиксное выражение. Общая форма инфиксного выражения — “OP operand1 operand2”.
Постфикс – в постфиксных выражениях сначала записываются операнды, за которыми следует оператор. Она имеет вид “operand1 operand2 OP”.

Рассмотрим выражение “a + b * c”. Компилятор сканирует выражение либо слева направо, либо справа налево. Заботясь о приоритете операторов и ассоциативности, он сначала сканирует выражение для вычисления выражения b * c. Затем снова придется сканировать выражение, чтобы добавить результат b * c к a.

По мере того, как выражения становятся все более и более сложными, такой подход повторного сканирования выражения становится неэффективным.

Чтобы преодолеть эту неэффективность, мы преобразуем выражение в постфикс или префикс таким образом, чтобы их можно было легко вычислить, используя структуру данных стека.

Читать также: Настройка среды разработки для C++

2) Синтаксический анализ / оценка выражений

Используя стек, мы также можем выполнять фактическую оценку выражения. В этом случае, выражение просматривается слева направо, а операнды помещаются в стек.

Всякий раз, когда встречается оператор, извлекаются операнды и выполняется операция. Результат операции снова помещается в стек. Это способ, при котором выражение вычисляется с помощью стека, и конечным результатом выражения обычно является текущая вершина стека.

3) Обход деревьев

Древовидная структура данных может быть пройдена для посещения каждого узла многими способами и в зависимости от того, когда посещается корневой узел, который у нас есть.

Обход по порядку
Обход предварительный
Пост обход

Для эффективного обхода деревьев мы используем структуру данных стека для перемещения промежуточных узлов в стеке, чтобы поддерживать порядок обхода.

4) Алгоритмы сортировки

Алгоритмы сортировки, такие как quicksort (быстрая сортировка), могут быть сделаны более эффективными с использованием структур данных стека.

5) Ханойские башни

Это классическая задача, включающая n дисков и три башни, и проблема заключается в перемещении дисков из одной башни в другую с использованием третьей башни в качестве промежуточной.

Эта проблема может быть эффективно решена с помощью стека, когда мы помещаем диски для перемещения в стек, поскольку стек в основном действует как башня, используемая для перемещения дисков.

Итог

Стек — это самая простая структура данных, которую проще реализовать в виде программы. В нем использовался подход LIFO (последний вход, первый выход), который означает, что элемент, введенный последним, удаляется первым. Так происходит потому, что стек использует только один конец для добавления (push) и удаления (pop) элементов.

Структура данных стека имеет много применений в программировании. Наиболее заметным среди них является оценка выражений. Вычисление выражения также включает преобразование выражения из инфиксного в постфиксный или префиксный. Это также включает в себя вычисление выражения для получения конечного результата.

В нашей следующей статье мы подробно изучим структуру данных очереди в C++.

С Уважением, МониторБанк

Основные операции

Демонстрация

Реализация

1) Использование массивов

2) Использование связного списка

Применения стека

1) Инфикс в постфиксные выражения

2) Синтаксический анализ / оценка выражений

3) Обход деревьев

4) Алгоритмы сортировки

5) Ханойские башни

Итог

Вам также может понравиться

Время писать первую программу на языке Паскаль

Типы наследования в C++

Строки, пары и кортежи в STL

Добавить комментарий Отменить ответ