Блог

Эффект практического (реального) индуктора в ограничении протекания тока обусловлен не только эффектом обратной ЭДС, который приводит к индуктивному реактивному сопротивлению X_L , но также частично обусловлен внутренним сопротивлением индуктора.

Поскольку эти две причины, возникающие в одном и том же компоненте, не могут быть физически разделены, часто важно учитывать совместное влияние как реактивного сопротивления, так и сопротивления на ток через катушку индуктивности.

Название, используемое для описания этого комбинированного противодействия протеканию тока, — это импеданс, который измеряется в Омах, но имеет символ Z.

Эта комбинация реактивного сопротивления и обычного сопротивления не является просто суммой этих величин. Например, чтобы получить импеданс простой последовательной цепи LR, сначала необходимо рассчитать фазную сумму сопротивления и реактивного сопротивления. Причину этого можно понять, изучив картинку ниже, на которой показана фазорная диаграмма для схемы, повторно нарисованной в виде прямоугольного треугольника.

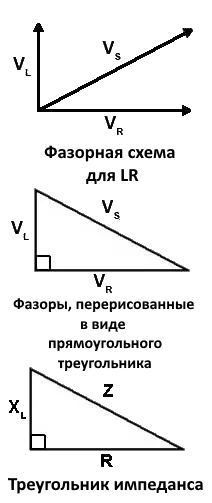
Три стороны треугольника представляют три фазы (вектора) напряжения в цепи V_R , V_L и V_S. Поскольку компоненты схемы расположены последовательно, один и тот же ток является общим для всех них.

Учитывая напряжения V_R и V_L на картинке выше, закон Ома гласит, что V_R = IR (ток, умноженный на сопротивление), поэтому V_L будет равен IX_L (ток, умноженный на реактивное сопротивление).

Теперь, поскольку Z — полное сопротивление всей цепи, общее напряжение в цепи, Vs = IZ

Поскольку эти вектора теперь образуют прямоугольный треугольник, теорема Пифагора может быть использована для связи всех этих векторов напряжения:

V_S ² = V_R ² + V_L ²

поэтому (поскольку V = IR и т.д.)

(IZ) ² = (IR) ² + (IX _L ) ² или I ² Z ² = I ² R ² + I ² X _L ²

Далее, деление на I² исключает I ² и дает Z ² = R ² + X _L²

и, извлекая квадратный корень из обеих сторон этого уравнения, получаем формулу для вычисления Z (полного сопротивления цепи LR).

При использовании этой формулы на калькуляторе важно не забывать использовать скобки или, в качестве альтернативы, находить сумму R² + X_L² перед использованием клавиши квадратного корня.

Помните, что импедансы, сопротивления и реактивные сопротивления сами по себе не являются векторными величинами. Они влияют на напряжения и токи, заставляя эти величины изменять свое отношение друг к другу, но поскольку Z, R и X сами по себе не меняются со временем, они не являются векторами.

На картинке ниже показано аналогичное соотношение, существующее в резистивной/емкостной цепи.

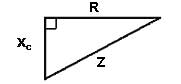
Диаграмма вектора напряжения для цепей CR может быть преобразована в прямоугольный треугольник и обработана так же, как диаграммы LR, представленные в самом верху, чтобы получить:

На картинке ниже показан еще один вариант треугольника импеданса, который можно использовать для расчета импеданса, когда в цепи присутствуют сопротивление (R), индуктивность (L) и емкость (C), а полное реактивное сопротивление (X) равно разнице между индуктивным реактивным сопротивлением (X_L ) и емкостным реактивным сопротивлением (X_C ).

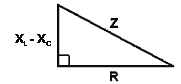
В этом случае формула для Z принимает вид:

Импеданс — это лишь одно из свойств, жизненно важных для понимания цепей переменного тока. Если вы изучили эту серию статей, а также серии статей про «Фазы и векторы» и «Реактивное сопротивление«, то вы должны начать понимать, как эти свойства работают вместе.

Чтобы понять, как импеданс зависит от других свойств цепи, таких как реактивное сопротивление, и увидеть, как импеданс влияет на такие параметры, как ток и напряжение, попробуйте выполнить некоторые расчеты с использованием приведенных формул.

В следующей статье поговорим о согласовании импедансов.

С Уважением, МониторБанк