Блог

Информация передается от одного места или человека к другому множеством различных способов. Каким бы способом ни передавалась информация, используемый сигнал принимает форму волн.

Это могут быть звуковые волны или электромагнитные (включая электрические или световые) волны, и хотя они могут физически сильно отличаться друг от друга, все они могут быть представлены в виде сигналов. Форма волны — это просто график, который показывает, как описанные свойства (например, звук или электричество) меняются со временем.

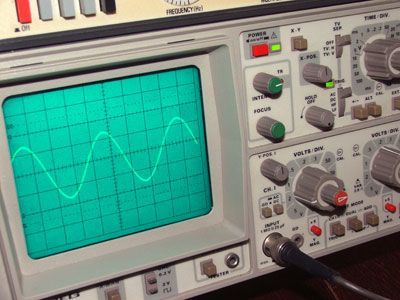
Со многими волнами, которые беспокоят инженеров-электронщиков, фактическую волну, действующую на высоких скоростях в электронных схемах, невозможно увидеть обычным способом, но такие инструменты, как осциллографы, могут рисовать графики этих «невидимых» волн и, таким образом, позволяют инженерам проверять, присутствует ли волна, и не искажена ли ее форма тестируемым оборудованием. Осциллограф также используется для измерения ряда свойств волн, предоставляя информацию о производительности оборудования.

Гармоники

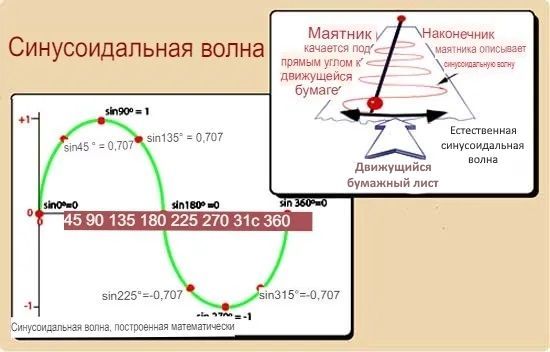
Формы сигналов, имеющие очень сложную форму, часто встречаются в электронном оборудовании, но все повторяющиеся волны, какими бы сложными они ни были, можно математически показать, что они состоят из серии гораздо более простых волн, каждая из которых имеет одинаковую форму. Эта форма волны называется синусоидальная волна, потому что ее график следует математической функции синуса. Форма синусоидальной волны довольно знакома, хотя обычно не распознается как таковая, поскольку ее форма волны или график плохо видны. Качающийся маятник часов — это пример синусоидальной волны, и многие естественные колебания являются синусоидальными (то есть «синусоидальной формы»).

Синусоидальные волны

На картинке выше показаны примеры синусоидальных волн, нанесенных математически на ряд вычисленных точек (внизу слева). Синусоидальную волну также можно создать естественным путем (вверху справа), прикрепив контейнер, такой как солонка, к концу качающегося маятника и перемещая лист цветной бумаги с постоянной скоростью под ним, когда он качается и высыпает соль. В результате получается красивая синусоидальная волна.

Таким образом, синусоидальная волна является математической функцией и естественной формой, она также является основой многих других форм волн и, следовательно, является наиболее важной формой волны при изучении теории переменного тока.

Сложные волны

Другими важными формами волн, обычно встречающимися в электронике, являются;

• Прямоугольная волна,
• Треугольная волна,
• Пилообразная волна.

Сложная волна — это волна, состоящая из серии синусоидальных волн; поэтому она более сложная, чем одна чистая синусоидальная волна. Эта серия синусоидальных волн всегда содержит волну, называемую «фундаментальной», которая имеет ту же частоту (частоту повторения), что и создаваемая комплексная волна.

Как и основная, комплексная волна содержит ряд гармоник. Это синусоидальные волны, которые имеют частоты, кратные целому числу фундаментальных; то есть фундаментальные х2, фундаментальные х3 и т.д. Основные и гармоники называются компонентами комплексной волны. В сложной волне часто присутствует еще один компонент, то есть компонент постоянного тока — это составляющая «волна», частота которой равна нулю, т.е.; на самом деле это не волна, а просто значение постоянного тока, которое влияет на результирующую комплексную волну. Можно показать, что квадратные, треугольные и пилообразные волны состоят из довольно простой серии компонентов, вы должны помнить, какая серия гармоник состоит, из каких именно из этих трех сложных волн.

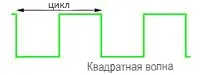
Прямоугольные волны

Прямоугольная волна содержит фундаментальную и ряд нечетных гармоник; то есть гармоники, которые являются нечетными числами, кратными фундаментальной (x3 x5 x7 и т.д.). Они называются 3-й гармоникой, 5-й гармоникой и т.д.

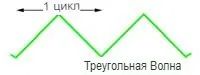
Треугольные волны

Треугольная волна также содержит основную и ряд нечетных гармоник, но в этом случае каждая последующая гармоническая составляющая начинается в фазе, противоположной предыдущей, т.е. 3-я гармоника начинается с положительной, 5-я гармоника начинается с отрицательной, 7-я с положительной и т.д. Это изменение фазы альтернативных гармоник является единственным отличием от компонентов прямоугольной волны, все гармоники которых начинаются в положительном направлении, но результирующие волны совершенно разные.

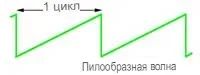
Пилообразные волны

Пилообразная волна содержит фундаментальную и четную и нечетную гармоники. В каждом из приведенных выше случаев основные и всего несколько гармонических составляющих придадут результирующей волне форму, приближенную к идеальной форме волны, показанной на картинке ниже. Чем больше гармоник включено в серию комплексных волн, тем лучше получается сложная форма волны, ближе к идеальной квадратной, треугольной или пилообразной форме.

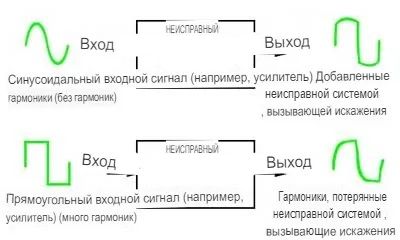
Этот факт важен для такого оборудования, как усилители Hi−Fi, поскольку при сложной форме сигнала на входе системы форма сигнала на громкоговорителе, в идеале, должна быть точно такой же формы, что и форма входного сигнала, чтобы создаваемый звук был как можно ближе к оригиналу. Это означает, что необходимо точно воспроизвести каждую синусоидальную составляющую исходной волны без «потери» каких-либо компонентов по пути.

Гармонические искажения

Система также не должна добавлять какие-либо гармоники, которых не было в исходном сигнале. В любом случае конечный выходной сигнал не будет иметь ту же форму, что и исходный, и в систему будут внесены нежелательные искажения.

На практике, можно игнорировать многие гармонические компоненты без заметного влияния на форму волны. Это связано с тем, что гармоники, наиболее близкие к основной частоте (2-я, 3-я и т.д.), имеют большие амплитуды и, следовательно, оказывают большее влияние на форму результирующей волны, высокочастотные гармоники (например, 15-я, 16-я) обычно очень малы по сравнению с более низкими гармониками и основными, поэтому они лишь очень незначительно изменяют результирующую волну.

В следующей статье мы с вами поговорим об измерении синусоидальной волны.

С Уважением, МониторБанк