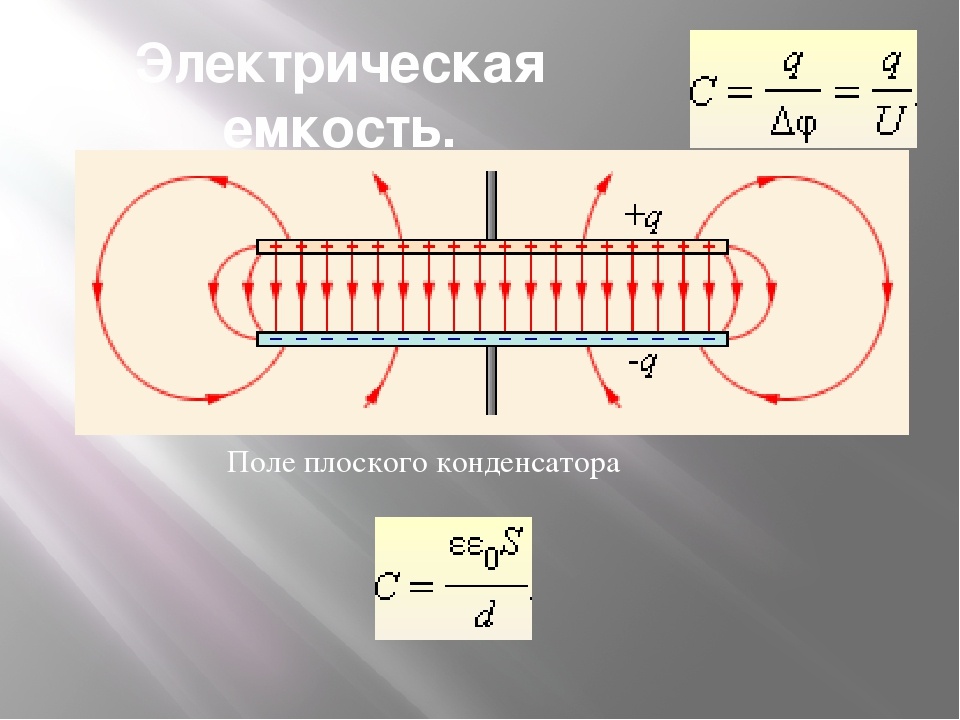
Емкость конденсатора определяется как способность конденсатора накапливать максимальный электрический заряд (Q) в своем теле. Заряд хранится в виде электростатической энергии. Емкость конденсаторов измеряется в единицах СИ- фарадах. Эти единицы могут быть обозначены в микрофарадах, нанофарадах, пикофарадах или фарадах. Формула для определения емкости конденсатора следующая:
C = Q/V = εA/d = ε0 εr A/d
Где,
C — емкость,
Q — заряд,
V — разность потенциалов между пластинами,
А — площадь между пластинами,
d — расстояние между пластинами.
ε — диэлектрическая проницаемость диэлектрика
ε0 — диэлектрическая проницаемость свободного пространства
εr — относительная диэлектрическая проницаемость свободного пространства
Собственная емкость
Свойство собственной емкости относится к конденсаторам с изолированным проводником. Как видно из названия, емкость — это свойство изолированного проводника повышать разность потенциалов до одного В. Обычно нормальные проводники имеют взаимную емкость. Это также измеряется в единицах СИ, то есть в фарадах.
Собственная емкость проводящей сферы радиусом R определяется выражением:
C = 4 π ɛ o R
Ниже приведены некоторые примеры значения собственной емкости:
- Для верхней пластины генератора Ван де Графа, имеющей радиус 20 см, собственная емкость составляет 22,24 пФ.
- Для планеты Земля собственная емкость составляет 710 мкФ.
Паразитная емкость
Паразитная емкость — это нежелательная емкость, т.е. шум. Даже такие компоненты, как резисторы, катушки индуктивности и провод, имеют свою некоторую емкость. Обычно на высоких частотах это приводит к появлению шума в цепи.
Паразитную емкость нельзя полностью устранить, но ее можно уменьшить. Разработчики схем должны позаботиться о паразитной емкости при проектировании схемы. Разделение и расстояние между компонентами и дорожками платы должно строго соблюдаться для уменьшения нежелательной емкости.
Она также измеряется в единицах СИ, то есть в фарадах.
Примерами являются: емкость между витками катушки, емкость между двумя соседними проводниками.
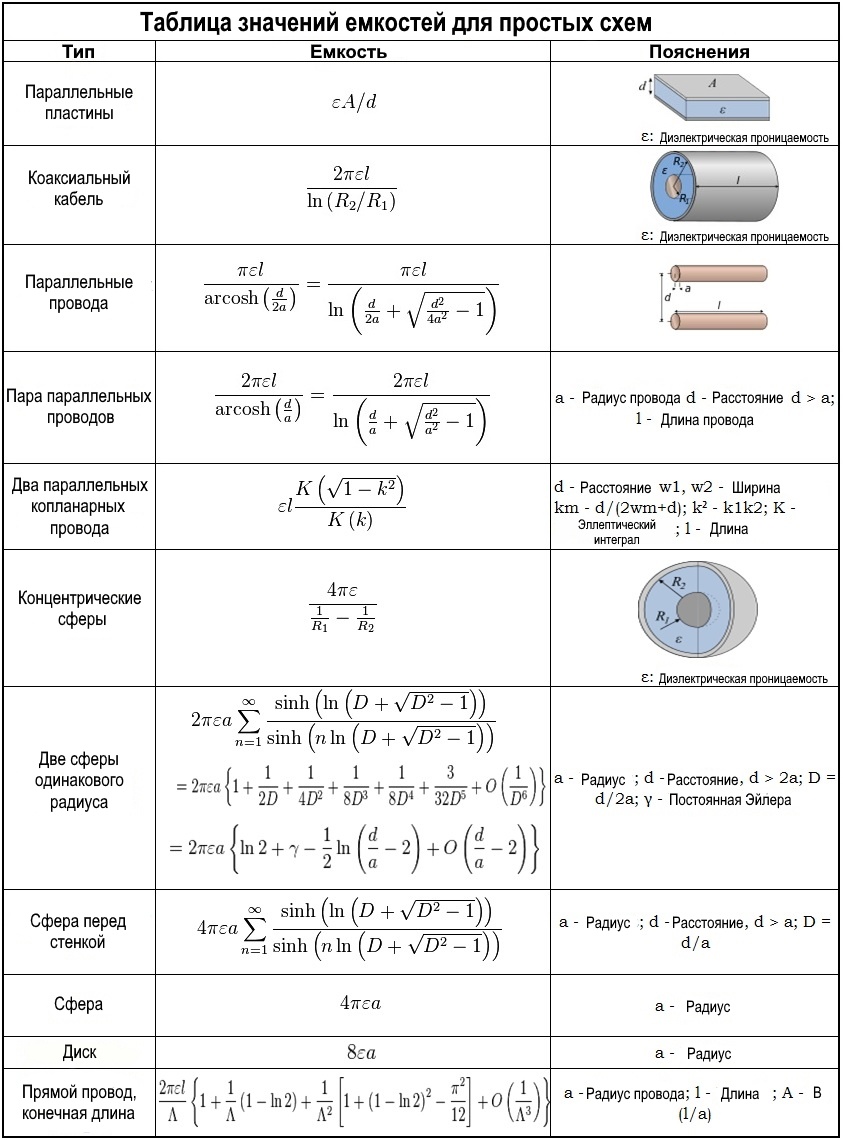
Емкость простых схем
Расчет емкости не что иное , как решение теоремы Лапласа ∇ 2 φ = 0 с постоянным потенциалом на поверхности конденсатора. Ниже приведены значения емкости для некоторых простых схем:
Заряд конденсатора
Способность конденсатора накапливать максимальный заряд (Q) на своих металлических пластинах называется его значением емкости (C). Полярность накопленного заряда может быть отрицательной или положительной, например, положительный заряд (+ ve) на одной пластине и отрицательный заряд (-ve) на другой пластине конденсатора. Выражения для заряда, емкости и напряжения приведены ниже.
C = Q/V, Q = CV, V = Q/C
Таким образом, заряд конденсатора прямо пропорционален его емкости и разности потенциалов между пластинами конденсатора. Заряд измеряется в кулонах. Один кулон заряда конденсатора можно определить как емкость в одну фараду между двумя проводниками, которые работают с напряжением в один вольт.
Заряд Q, накопленный в конденсаторе, имеющем емкость C, разность потенциалов V и воздух в качестве его диэлектрика, определяется выражением:
Q = CV = (ε × (A × V))/d
Где,
ε0 — диэлектрическая проницаемость свободного пространства,
εr — относительная диэлектрическая проницаемость диэлектрического материала,
ε — диэлектрическая проницаемость диэлектрического материала.
Из двух вышеупомянутых случаев мы можем наблюдать:
Заряд конденсатора прямо пропорционален площади пластин, диэлектрической проницаемости диэлектрического материала между пластинами и обратно пропорционален расстоянию между пластинами. Таким образом, чем больше площадь пластин, тем больше заряд конденсатора, а чем больше расстояние между пластинами, тем меньше заряд конденсатора.
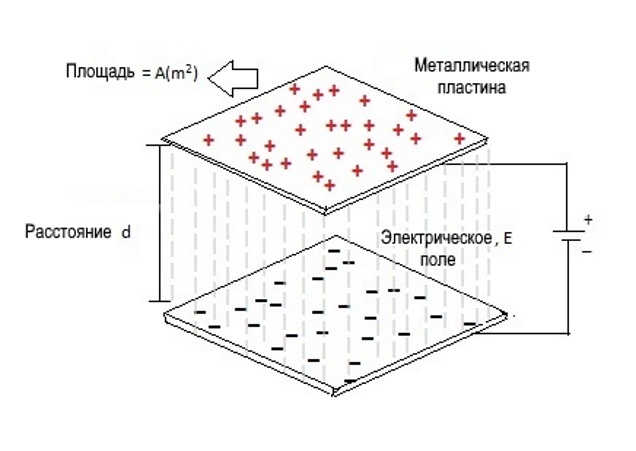
Параллельный пластинчатый конденсатор
На приведенном выше рисунке показана схема конденсатора с параллельными пластинами. Как мы знаем, емкость прямо пропорциональна площади пластин (A) и обратно пропорциональна расстоянию (d) между двумя металлическими пластинами. Значение емкости конденсатора с параллельными пластинами определяется выражением:
C = k ε0A/d
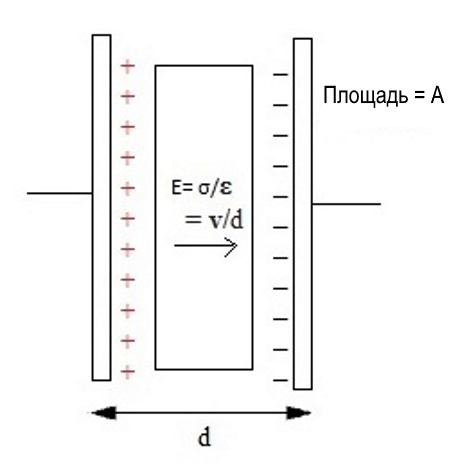
Где, k — диэлектрическая проницаемость, а ε0 — диэлектрическая проницаемость свободного пространства, равная 8,854 · 10 -12 Ф/м. Диэлектрическая постоянная (k) — это параметр, связанный с диэлектрическим материалом, который увеличивает емкость по сравнению с воздухом. Чем больше площадь поверхности пластин, тем больше значение емкости, и наоборот. Еще один пример схемы конденсатора с параллельными пластинами показан на рисунке ниже.
Пример емкости №1
Теперь мы рассчитаем емкость конденсатора с параллельными пластинами в пикофарадах, у которого площадь поверхности пластин составляет 200 см2, и они разделены воздухом в качестве его диэлектрического материала с расстоянием 0,4 см.
Уравнение емкости конденсатора с параллельными пластинами выглядит следующим образом:
C = A/d
ε = 8,854 X 10-12Ф / м.
A = 200 см2 = 0,02 м2
D = 0,4 см = 0,004 м
Теперь мы подставляем эти значения в приведенное выше уравнение:
C = 8,854 X 10-12 * (0,02 м2 / 0,004 м) = 44,27 пФ
И получаем, емкость конденсатора с параллельными пластинами составляет 44,27 пФ.
Зарядка и разрядка конденсатора
Схема ниже используется для объяснения заряда и разряда конденсатора. Предположим, что конденсатор, который показан на схеме, полностью разряжен. В этой схеме емкость конденсатора составляет 100 мкФ, а напряжение питания, подаваемое на эту схему, составляет 12 В.
Теперь переключатель, который подключен к конденсатору в цепи, перемещается в точку A. Затем конденсатор начинает заряжаться зарядным током (i). Напряжение зарядки на конденсаторе равно напряжению питания, когда конденсатор полностью заряжен, то есть VS = VC = 12 В. Когда конденсатор полностью заряжен, это означает, что конденсатор поддерживает заряд с постоянным напряжением, даже если напряжение питания отключено от цепи.
В случае идеальных конденсаторов, заряд на конденсаторе остается постоянным, но в случае обычных конденсаторов полностью заряженный конденсатор медленно разряжается из-за его тока утечки.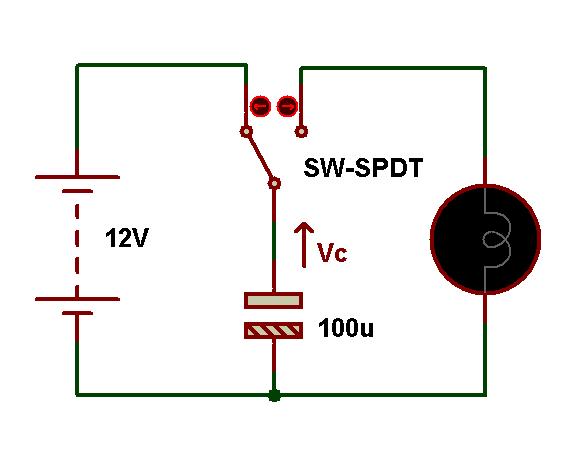
Когда переключатель перемещается в положение B, конденсатор медленно разряжается за счет включения лампы, которая помещена в цепь. Наконец-то он полностью разряжен до нуля. Сначала лампа ярко светится, когда конденсатор полностью заряжен, но яркость лампы уменьшается по мере уменьшения заряда конденсатора.
Пример заряда конденсатора №2
Теперь давайте вычислим заряд конденсатора в приведенной выше схеме. Уравнение заряда конденсатора имеет следующий вид:
Q = CV
C = 100 мкФ
V = 12V
Теперь мы подставляем эти значения в приведенное выше уравнение:
Q = 100 мкФ * 12 В = 1,2 мкФ
Следовательно, заряд конденсатора в приведенной выше схеме составляет 1,2 мКл.
Ток протекающий через конденсатор
Ток (i), протекающий через любую электрическую цепь, — это скорость заряда (Q), протекающего через нее, относительно времени. Но заряд конденсатора прямо пропорционален приложенному через него напряжению. Соотношение между зарядом, током и напряжением конденсатора приведено в уравнении ниже:
I (t) = d Q (t) / dt = C dV (t) / dt
Мы знаем, что:
Q = CV
V = Q / C
V (t) = Q (t) / C
Q (t) = CV (t)
Отношение тока к напряжению определяется выражением:
I (t) = C dV (t) / dt
Из этого соотношения мы можем заметить, что ток, протекающий через конденсатор в цепи, является произведением емкости и скорости изменения напряжения, приложенного к цепи. Ток, протекающий через конденсатор, прямо пропорционален емкости конденсатора и величине напряжения.
Чем больше ток, тем выше емкость цепи и чем выше приложенное напряжение, тем больше ток, протекающий по цепи. Если напряжение постоянное, то и заряд постоянен, поэтому заряд не протекает. Следовательно, ток, протекающий по цепи, станет нулевым.
Единица емкости (Фарад)
Джозия Латимер Кларк в 1861 году впервые использовал термин Фарад. Фарад — стандартная единица измерения емкости. Это очень большая единица измерения емкости.
Емкость одна фарада определяется как емкость с одним кулоном заряда, работающая при напряжении в один вольт.
C = Q / V
1Фарад = 1Кулон / 1В
Сейчас доступны конденсаторы с большой емкостью в сотни фарад. Эти конденсаторы с высокими значениями емкости называются «суперконденсаторами». В этих конденсаторах используется большая площадь поверхности для передачи высокой энергии, поскольку они имеют высокие значения емкости.
При низком напряжении суперконденсаторы обладают способностью накапливать большую энергию с высокими значениями емкости. Эти высокоэнергетические суперконденсаторы используются в переносных портативных устройствах для замены больших, тяжелых и дорогих конденсаторов литиевого типа, поскольку они хранят большую энергию, как батареи. Эти конденсаторы также используются в аудио- и видеосистемах в транспортных средствах для замены высоковольтных батарей.
Разделение Фарада
Стандартная единица измерения емкости — фарады. Но это очень большая единица измерения емкости. В этом фараде есть несколько дополнительных единиц; это микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ).
1 мкФ (мкФ) = (1/1000000) Ф = 10-6 Ф
1нано-Фарад (мкФ) = (1/1000000000) Ф = 10-9 Ф
1 пико-Фарад (мкФ) = (1/1000000000000) Ф = 10-12 Ф
Теперь мы увидим некоторые преобразования между единицами измерения емкости,
(i) преобразование 33 пФ в нФ => 33 пФ = 0,033 нФ
(ii) преобразование 22 нФ в мкФ => 22 нФ = 0,022 мкФ
(iii) преобразование 11 мкФ в Ф => 11 мкФ = 0,11 Ф
Энергия в конденсаторе
Энергия — это количество некоторой работы против электростатического поля для полной зарядки конденсатора. В конденсаторе на начальной стадии зарядки заряд Q передается между пластинами с одной пластины на другую. Этот заряд либо + Q, либо –Q меняется местами между двумя пластинами конденсатора. После преобразования некоторого заряда между пластинами образуется электрическое поле, в этом случае нам потребуется дополнительная работа, чтобы зарядить конденсатор полностью. Эта дополнительная работа называется энергией, запасенной в конденсаторе. Энергия измеряется в джоулях (Дж). Теперь мы приведем уравнения для этой энергии и работы:
dW = V dQ
dW = (Q / C) dQ
После интегрирования приведенного выше уравнения:
W = Q 2 / 2C
W = (CV) 2 / 2C
W = CV 2 /2 Джоулей
Наконец, мы получаем, что энергия, хранящаяся в конденсаторе, равна:
Энергия (W) = CV 2 /2 Джоулей
Теперь посчитаем энергию, запасенную в конденсаторе емкостью 200 мкФ, работающего с напряжением 12 В.
W = CV 2 /2
W = (200 × 10-6 × 12 2 ) / 2 = 14,4 м Дж
Вот и все, что вам нужно было знать о емкости и заряде конденсатора. Если вам нравятся наши статьи, то оставляйте свои комментарии.
С Уважением, МониторБанк