 Помимо использования функций для разбиения кода на части для упрощения и удобочитаемости кода, функции полезны в различных других приложениях, включая решение задач в реальном времени, математические и статистические вычисления.
Помимо использования функций для разбиения кода на части для упрощения и удобочитаемости кода, функции полезны в различных других приложениях, включая решение задач в реальном времени, математические и статистические вычисления.
По мере создания более сложных приложений на C++, мы можем столкнуться с различными требованиями, поэтому нам будет необходимо использовать несколько специальных концепций C++. Рекурсия является одной из них.
Что такое рекурсия?
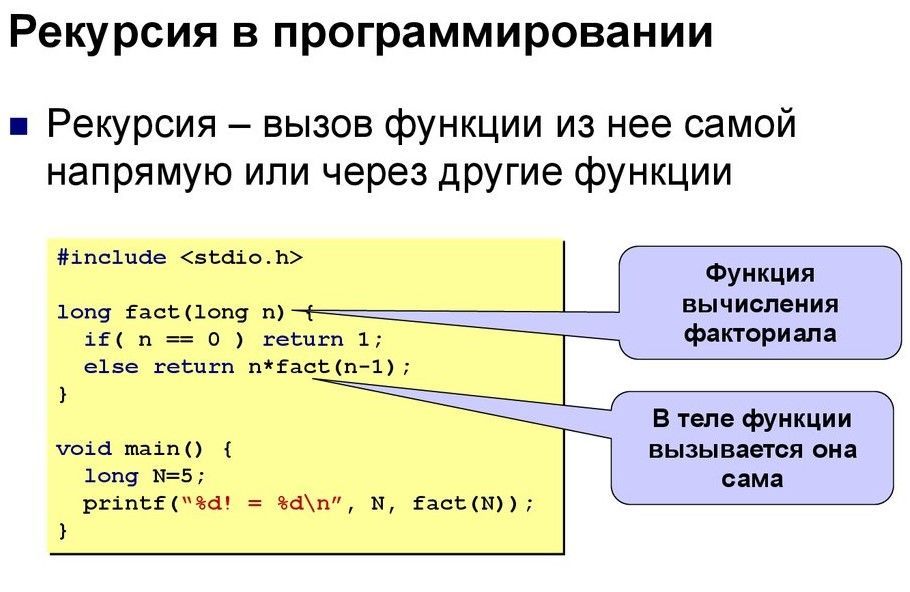
Рекурсия — это процесс, в котором функция вызывает сама себя. Функция, реализующая рекурсию или вызывающая сама себя, называется рекурсивной функцией. В рекурсии рекурсивная функция вызывает себя снова и снова и продолжает работать до тех пор, пока не будет выполнено конечное условие.
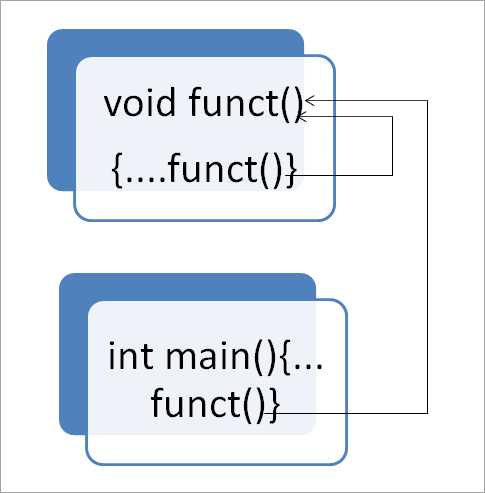
На изображении ниже показана работа рекурсии:
Как вы можете видеть на диаграмме выше, основная функция вызывает функцию funct(). Функция funct(), в свою очередь, вызывает себя внутри своего определения. Вот как работает рекурсия. Этот процесс вызова функции будет продолжаться до тех пор, пока мы не обеспечим завершающее условие, которое и завершит его.
Обычно предоставляется ветвь кода при реализации рекурсии, так что мы предоставляем одно условие, которое запускает рекурсию, и другое, чтобы выполнять обычное выполнение.
Базовое условие рекурсии
При выполнении рекурсии предоставляется решение для базового или завершающего случая, а решения более крупных задач строятся на основе решений более мелких задач.
Рассмотрим классический пример рекурсии, факториальную нотацию.
Мы знаем, что математически факториал числа n равен:
n! = nxn-1x….x0!
учитывая что 0! = 1;
Так что факториал для n=3 будет равен 3! = 3×2!
3! = 3x2x1!
3! = 3x2x2x0!
3! = 3x2x1x1 = 6
Таким образом, программно мы можем выразить это вычисление следующим образом:
|
1 2 3 4 5 6 |
int factorial(int n){ if(n <=1) return 1; else return n*factorial(n-1); } |
Таким образом, как показано выше, мы выразили приведенное выше вычисление факториала в рекурсивном вызове функции. Мы видим, что если число n меньше или равно 1, мы возвращаем 1 вместо рекурсивного вызова. Это называется базовым условием/случаем для факториала, который позволяет остановить рекурсию.
Следовательно, базовое условие в основном определяет, сколько раз рекурсивная функция должна вызывать себя. Это означает, что мы можем вычислить факториал большего числа, выражая его через меньшие числа, пока не будет достигнут базовый класс.
Ниже приведен пример для вычисления факториала числа:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
#include <iostream> #include <string> using namespace std; int factorial(int n){ if(n <=1) return 1; else return n*factorial(n-1); } int main() { int num,result; cout<<"Enter the number whose factorial is to be calculated:"; cin>>num; result = factorial(num); cout<<num<<"! = "<<result; return 0; } |
Вывод данных:
|
1 2 |
Enter the number whose factorial is to be calculated:10 10! = 3628800 |
В приведенном выше примере мы реализуем рекурсию. Берем число, факториал которого нужно найти, из стандартного ввода и передаем его функции факториала.
В факториальной функции мы задали базовое условие как (n<=1). Итак, когда базовый случай достигнут, функция возвращается. Используя этот базовый случай, мы можем вычислить факториал любого числа больше 1.
Выделение памяти для рекурсивного вызова
Мы знаем, что при вызове функции состояние вызывающей функции сохраняется в стеке, а когда вызов функции завершается, это состояние восстанавливается, чтобы программа могла продолжить выполнение.
Когда выполняется рекурсивный вызов функции, состояние или память для вызываемой функции выделяется поверх состояния вызывающей функции, и для каждого вызова рекурсивной функции создается другая копия локальных переменных.
Когда базовое условие достигнуто, функция возвращается к вызывающей функции, память освобождается, и процесс продолжается.
Переполнение стека в рекурсии
Когда рекурсия продолжается неограниченное время, это может привести к переполнению стека.
Когда рекурсия может так продолжаться? Первое, когда мы не указываем базовое условие. Второе, когда базовое условие не достигается при выполнении программы.
Пример, мы модифицируем приведенную выше факториальную программу и изменим ее базовое условие:
|
1 2 3 4 5 6 |
int factorial(int n){ if(n ==1000) return 1; else return n*factorial(n-1); } |
В приведенном выше коде мы изменили базовое условие на (n==1000). Теперь, если мы присвоим число n = 10, мы можем заключить, что базовое условие никогда не будет достигнуто. Таким образом, в какой-то момент память в стеке будет исчерпана, что приведет к переполнению стека.
Следовательно, при разработке рекурсивных программ нужно быть осторожными с базовым условием, которое мы предоставляем.
Прямая и косвенная рекурсия
До сих пор в рекурсии мы видели функцию, вызывающую саму себя. Она называется прямая рекурсия.
Существует еще один тип рекурсии, т.е. непрямая рекурсия. В этом случае функция вызывает другую функцию, а затем эта функция вызывает вызывающую функцию. Если f1 и f2 — две функции. Затем f1 вызывает f2, а f2, в свою очередь, вызывает f1. Это косвенная рекурсия.
Давайте пересмотрим нашу факториальную программу для демонстрации прямой рекурсии:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
#include <iostream> #include <string> using namespace std; int factorial_b(int); int factorial_a(int n){ if(n <=1) return 1; else return n*factorial_b(n-1); } int factorial_b(int n){ if(n <=1) return 1; else return n*factorial_a(n-1); } int main() { int num, result; cout<<"Enter the number whose factorial is to be calculated:"; cin>>num; result = factorial_a(num); cout<<num<<"! = "<<result; return 0; } |
Вывод данных:
|
1 2 |
Enter the number whose factorial is to be calculated:5 5! = 120 |
В приведенном выше примере мы показали косвенную рекурсию. Основная функция вызывает factorial_a. Factorial_a вызывает factorial_b. В свою очередь, factorial_b вызывает factorial_a. Мы видим, что на вывод программы это не влияет.
Хвостовая и не хвостовая рекурсия
Хвостовая рекурсивная функция — это рекурсивная функция, в которой выполняется последний вызов функции.
Например, рассмотрим следующую функцию:
|
1 2 3 4 5 6 |
void display(int n){ if(n<=1) return; cout<<” \t”<<n; display(n-1); } |
В приведенном выше примере отображение является хвостовой рекурсивной функцией, так что это последний вызов функции.
Хвостовые функции считаются лучше рекурсивных функций без хвостов, поскольку они могут быть оптимизированы компилятором. Причина в том, что, поскольку хвостовой рекурсивный вызов является последним оператором в функции, после этого вызова не выполняется никакого кода.
В результате сохранение текущего кадра стека для функции не требуется.
Плюсы и минусы рекурсии перед итеративным программированием
Рекурсивные программы обеспечивают компактный и чистый код. Рекурсивная программа — это простой способ написания программ. Есть некоторые неотъемлемые проблемы, такие как факториал, последовательность Фибоначчи, ханойские башни и т.д., которые требуют рекурсии для решения.
Другими словами, они эффективно решаются с помощью рекурсии. Их также можно решить с помощью итеративного программирования с использованием стеков или других структур данных, но есть вероятность, что они станут более сложными для реализации.
Рекурсивные возможности рекурсивного и итеративного программирования одинаковы. Однако рекурсивные программы занимают больше места в памяти, так как все вызовы функций должны храниться в стеке до тех пор, пока не будет сопоставлен базовый случай.
Рекурсивные функции также требуют дополнительных затрат времени из-за слишком большого количества вызовов функций и возвращаемых значений.
Примеры рекурсии
Далее мы реализуем некоторые примеры рекурсивного программирования.
Числа Фибоначчи
Ряд Фибоначчи — это последовательность, которая задается как:
0 1 1 2 3 5 8 13……
Как показано выше, первые два числа ряда Фибоначчи — это 0 и 1. Следующее число в последовательности — это сумма двух предыдущих чисел.
Давайте реализуем эту последовательность, используя рекурсию:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
#include<iostream> using namespace std; void fibSeries(int n){ static int n1=0, n2=1, n3; if(n>0){ n3 = n1 + n2; n1 = n2; n2 = n3; cout<<n3<<" "; fibSeries(n-1); } } int main(){ int num; cout<<"Enter the number of elements for Fibonacci series: "; cin>>num; cout<<"Fibonacci Series for "<<num<<" numbers: "; cout<<"0 "<<"1 "; fibSeries(num-2); return 0; } |
Вывод данных:
|
1 2 |
Enter the number of elements for Fibonacci series: 10 Fibonacci Series for 10 numbers: 0 1 1 2 3 5 8 13 21 34 |
В этом примере мы использовали рекурсивный вызов для генерации последовательности Фибоначчи. Вы можете видеть, что первые два числа, являющиеся постоянными, печатаются напрямую, а для следующих чисел в последовательности мы используем рекурсивную функцию.
Палиндром
Число-палиндром — это число, которое при чтении в обратном направлении совпадает с чтением в направлении слева направо.
Например, число 121 при чтении слева направо и справа налево читается одинаково, т.е. 121. Следовательно, 121 является палиндромом.
Число 291 при чтении справа налево, т.е. в обратном порядке, читается как 192. Следовательно, 291 не является палиндромом.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
#include <iostream> using namespace std; int reverse_digits(int n, int temp) { if (n == 0) return temp; temp = (temp * 10) + (n % 10); return reverse_digits(n / 10, temp); } int main() { int num; cout<<"Enter the number to check palindrome:"; cin>>num; int result = reverse_digits(num, 0); if (result == num) cout << "Number "<<num<<" is a palindrome" << endl; else cout << "Number "<<num<<" is not a palindrome"<< endl; return 0; } |
Вывод данных:
|
1 2 |
Enter the number to check palindrome:6556 Number 6556 is a palindrome |
В приведенной выше программе мы считываем входной номер со стандартного ввода. Затем мы передаем это число рекурсивной функции, чтобы поменять местами цифры числа. Если перевернутые цифры и входное число совпадают, то число является палиндромом.
Вывод
На этом мы закончили с рекурсией. В данной статье мы подробно изучили рекурсивное программирование, рекурсивную функцию, ее преимущества и недостатки, а также различные примеры.
Помимо этих примеров, рекурсия также используется при решении некоторых стандартных задач, таких как обходы (inorder/preorder/postorder), ханойские башни, обход BFS и т. д. В следующей статье изучим указатели и их использование в C++.
С Уважением, МониторБанк