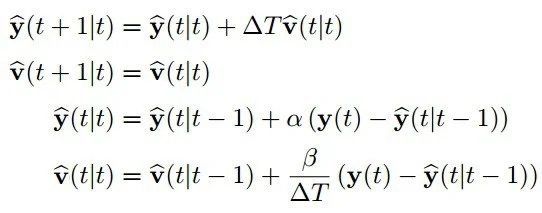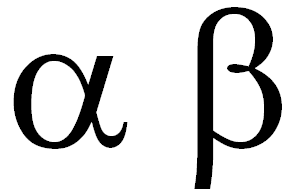Задача датчиков — предоставить информацию о положении робота и других объектов. Эти данные передаются в алгоритмы управления. Сигналы с датчиков ошибочные. Но, чтобы получить более подробную информацию о состоянии объекта, его оценка должна производиться на основании данных измерений.
Введение
Популярным методом решения этой проблемы, является фильтрация Калмана (кто уже об этом хоть что-то знает, тот поймет). Это статистически оптимальный метод оценки состояния. Это означает, что при заданных рабочих параметрах нет более точной оценки состояния объекта. Однако его реализация требует знания модели состояния объекта и ковариационной матрицы ошибок измерения и обработки, а также выполнения вычислений с матрицами. Поэтому мы бы хотели предложить упрощенный метод, который, однако, может дать очень хорошие результаты на практике.
Фильтр Alpha — Beta
Фильтр альфа-бета основан на предположении, что движение объекта может быть выражено в двух компонентах состояния, где один компонент является производным от другого. Вектор состояния, состоящий из значения положения и скорости, удовлетворяет этим предположениям. Уравнения фильтра принимают вид:
Где y ^ — оценка положения, v — оценка скорости, y — измеренное положение, а ΔT — временной шаг между последовательными измерениями.
Выражение (t | t) означает значение в текущий момент времени на основе измерения до текущего момента времени, (t + 1 | t) означает значение в следующий момент времени на основе измерений до текущего момента времени. Момент времени, а (t | t-1) означает значение в текущий момент времени, основанное на измерениях до предыдущего момента времени.
Алгоритм делится на этап прогнозирования следующего состояния (первые два уравнения) и корректировку прогнозируемого значения на основе измерения (следующие два уравнения). Параметры альфа и бета используются для настройки фильтра. Их значения следует менять в диапазоне от 0 до 1.
Выполнение
Чтобы представить алгоритм на практике, мы написали простой скрипт на Matlab:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
% Параметры моделирования dt = 0.1; t_end = 10; t = 0:dt:t_end; % Параметрический фильтр alfa = 0.1; beta = 0.05; Y = zeros(1, size(t,2)); Yf = Y; ypri = 0; ypost = 0; vpri = 0; vpost = 0; for i = 1:size(t,2) if i < 50 Y(i) = 10*randn(1); else Y(i) = 10*randn(1) + 100; end ypri = ypost + dt*vpost; vpri = vpost; ypost = ypri + alfa*(Y(i) - ypri); vpost = vpri + beta*(Y(i) - ypri)/dt; Yf(i) = ypost; end plot(t, Y, 'b', t, Yf, 'r', 'LineWidth', 1.5) title('Фильтр alfa-beta') xlabel('Время') ylabel('Измеренный сигнал') legend('Измеренное значение', 'Оценочное значение') |
Измеренный сигнал представляет собой случайный сигнал с ожидаемым значением 0 и дисперсией 10. Через 5 секунд ожидаемое значение увеличивается до 100.
Фильтр альфа-бета содержится в четырех строках кода:
|
1 2 3 4 |
ypri = ypost + dt*vpost; vpri = vpost; ypost = ypri + alfa*(Y(i) - ypri); vpost = vpri + beta*(Y(i) - ypri)/dt; |
Результаты симуляции
Моделирование для альфа = 0,1 и бета = 0,05 дало следующий результат:
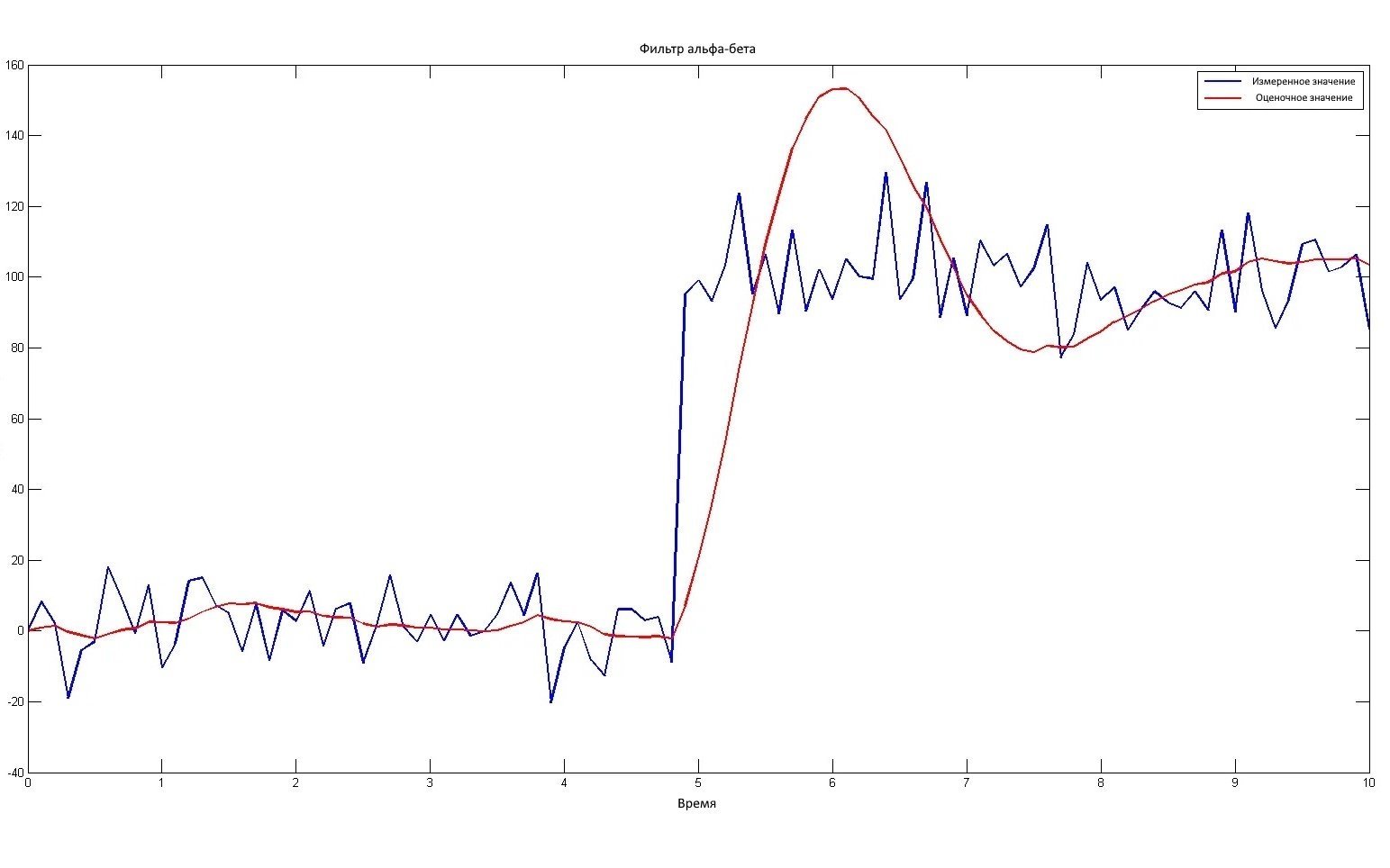
Мы видим, что в начальной фазе фильтр показывает значения, близкие к нулю, так что помехозащищенность хорошая. Проблема начинается после скачка ожидаемого значения. Тогда мы можем наблюдать большую задержку и выброс.
Моделирование
Мы сделали еще одно моделирование для значений альфа = 0,1 и бета = 0,2:
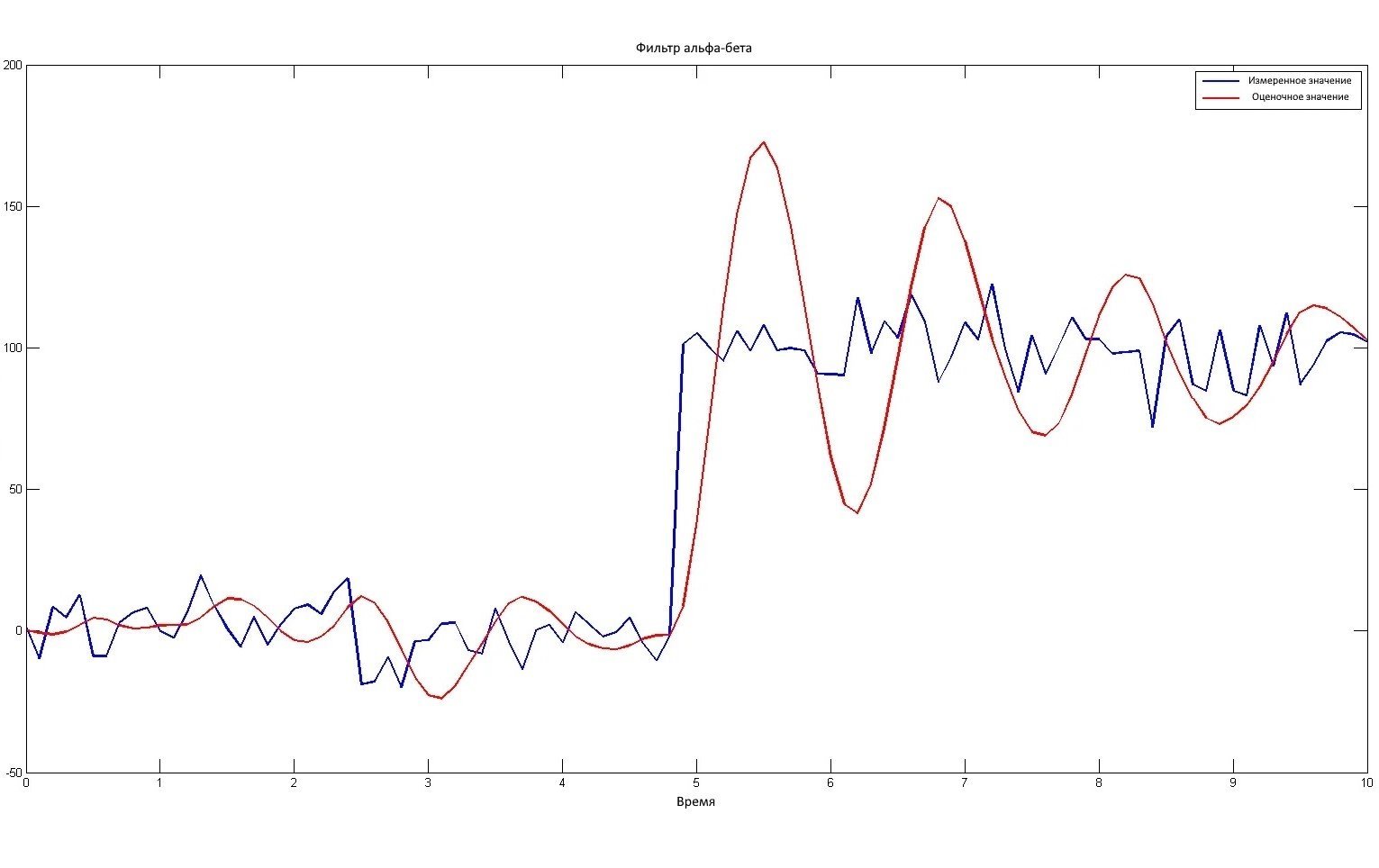
В этом случае перерегулирование определенно больше, чем раньше. Вдобавок мы видим, что устойчивость к большим шаговым возмущениям в первой фазе намного хуже, чем раньше.
| Это эффект увеличения параметра бета. |
В следующем моделировании мы установили альфа = 0,7, бета = 0,05:
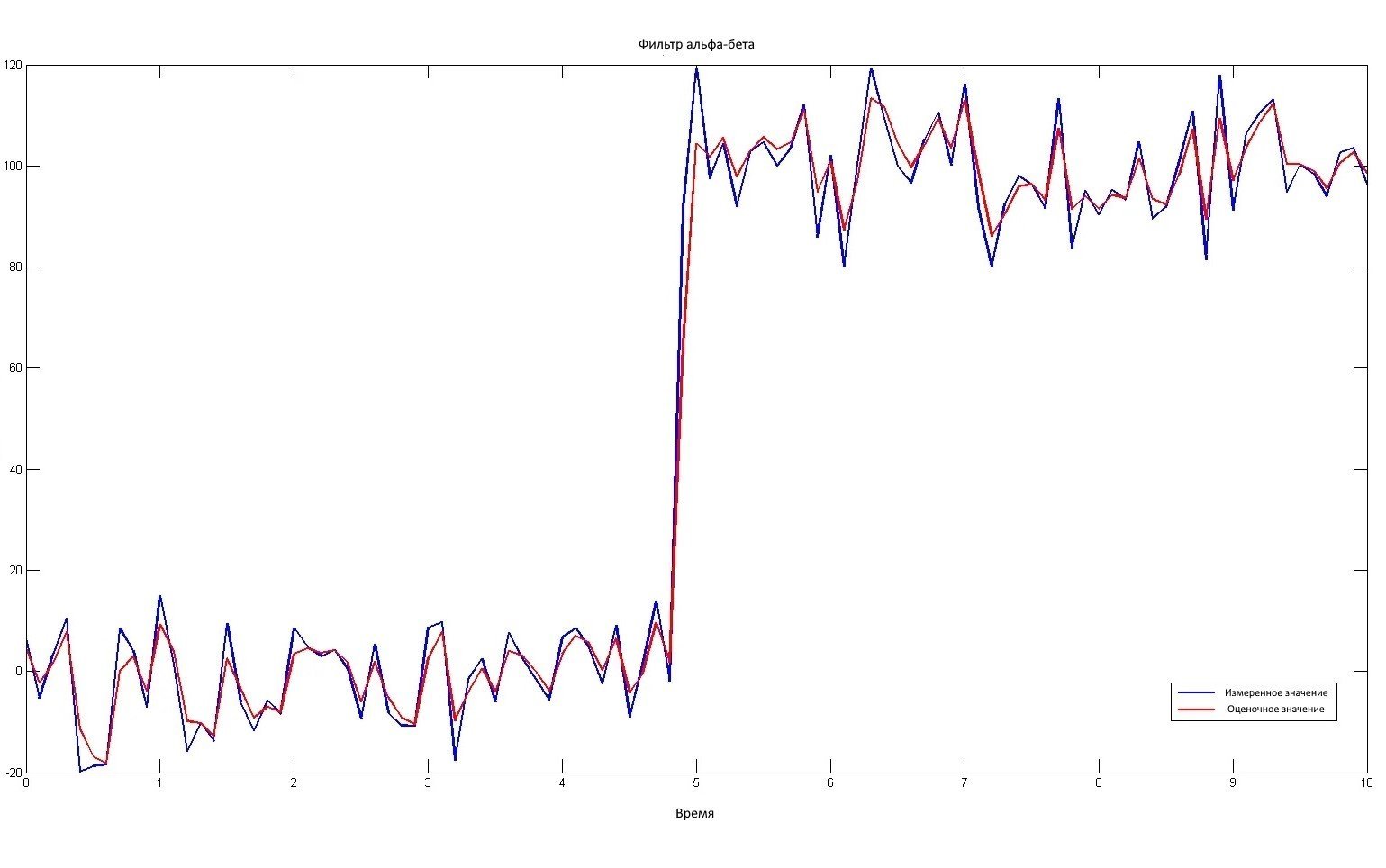
Мы видим, что отфильтрованные значения не сильно отличаются от измеренных значений. В результате фильтр имеет низкую помехоустойчивость, но быстро реагирует на резкие изменения сигнала.
В последней симуляции мы установили альфа = 0,35, бета = 0,05:
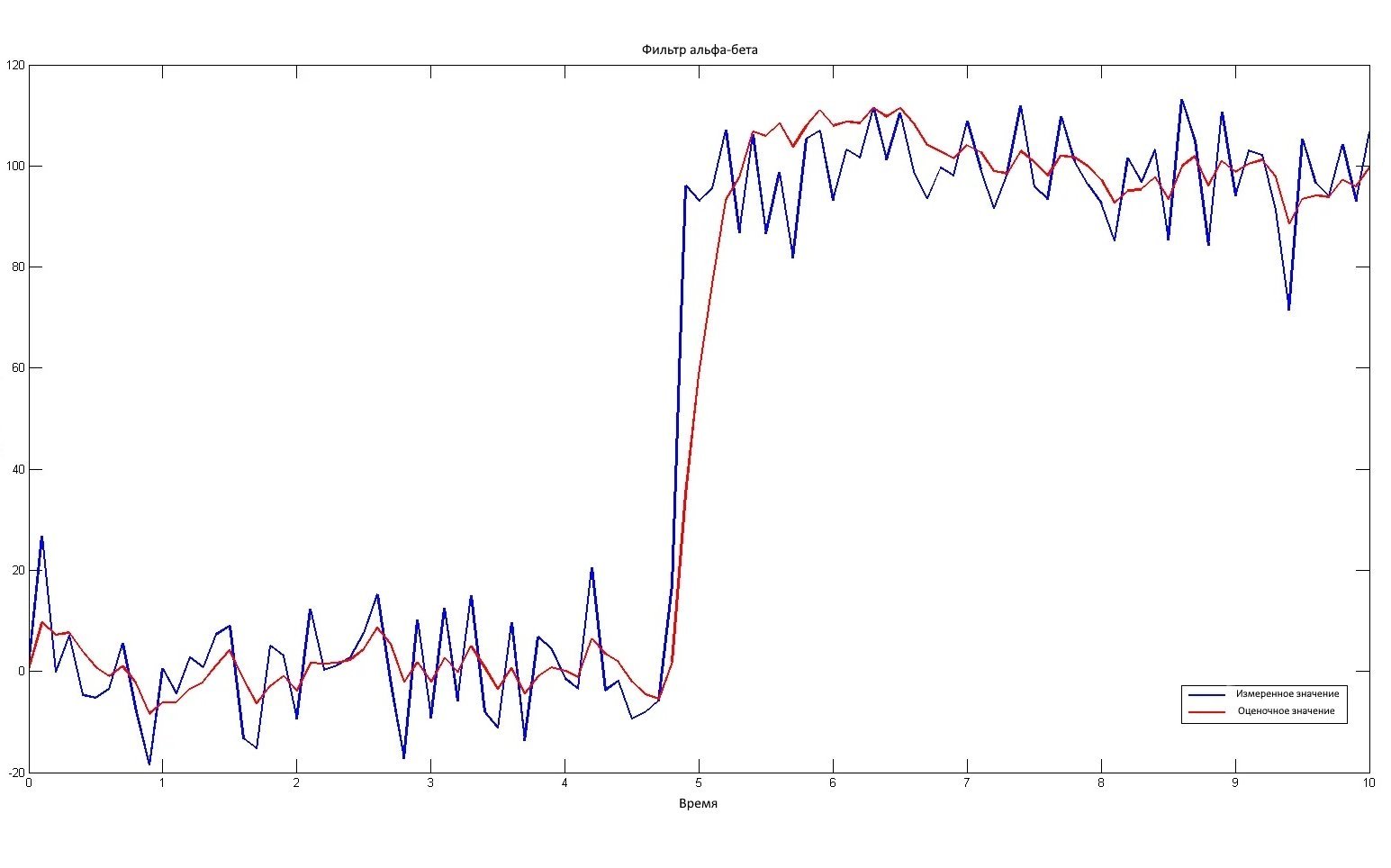
На этот раз показатели у нас хуже, чем раньше, на скачкообразное изменение сигнала, но помехозащищенность определенно лучше.
Вывод
Как видно из моделирования, низкие значения параметра альфа обеспечивают высокую невосприимчивость к помехам датчика за счет более медленной реакции на скачкообразные изменения сигнала. Увеличение значения альфа улучшает время отклика и ухудшает помехозащищенность. Лучше всего назначать бета-параметру небольшие значения. Его увеличение снижает стабильность фильтра.
В следующей части статьи мы рассмотрим практическую реализацию альфа-бета-фильтра с гироскопом и микроконтроллером STM32 .
С Уважением, МониторБанк