Сортировка вставками — это метод сортировки, который можно сравнить с игрой в карты. Точно так же, как мы вкладываем любую карту в колоду или вытаскиваем ее, сортировка вставками работает аналогичным образом.
Метод алгоритма сортировки вставками более эффективен, чем методы пузырьковой сортировки и сортировки выбором, но менее эффективен, чем другие методы, такие как быстрая сортировка и сортировка слиянием.
В методе сортировки вставками мы начинаем работу со второго элемента, сравниваем его с первым элементом и помещаем в нужное место. Затем, выполняем этот процесс для последующих элементов.
Мы сравниваем каждый элемент со всеми его предыдущими элементами и помещаем или вставляем элемент в правильное место. Метод сортировки вставками лучше подходит для массивов с меньшим количеством элементов. Этот метод также поможет для сортировки связных списков.
Связные списки имеют указатель на следующий элемент (в случае односвязного списка) и указатель на предыдущий элемент (в случае двусвязного списка). Следовательно, становится проще реализовать сортировку вставками для связного списка.
Общий алгоритм
Шаг 1: Повторить шаги с 2 по 5 для K = 1 до N-1
Шаг 2: установить температуру = A[K]
Шаг 3: установить J = K – 1
Шаг 4: Повторить, пока температура <=A[J]
установить A[ J + 1] = A[J]
установить J = J – 1
[конец внутреннего цикла]
Шаг 5: установить A[J + 1] = temp
[конец цикла]
Шаг 6: вывод данных
Таким образом, в методе сортировки вставками мы начинаем со второго элемента, поскольку предполагаем, что первый элемент всегда сортируется. Затем от второго элемента до последнего элемента сравниваем каждый элемент со всеми его предыдущими элементами, и помещаем этот элемент в нужное место.
Псевдокод
Псевдокод для сортировки вставками приведен ниже:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
procedure insertionSort(array,N ) array – array to be sorted N- number of elements begin int freePosition int insert_val for i = 1 to N -1 do: insert_val = array[i] freePosition = i //найти свободное положение для вставки элемента whilefreePosition> 0 and array[freePosition -1] >insert_val do: array [freePosition] = array [freePosition -1] freePosition = freePosition -1 end while //вставить номер в свободную позицию array [freePosition] = insert_val end for end procedure |
Выше приведен псевдокод для сортировки вставками, далее мы продемонстрируем эту технику на следующем примере:
Демонстрация
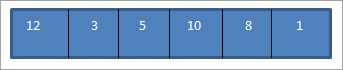
Массив для сортировки выглядит следующим образом:
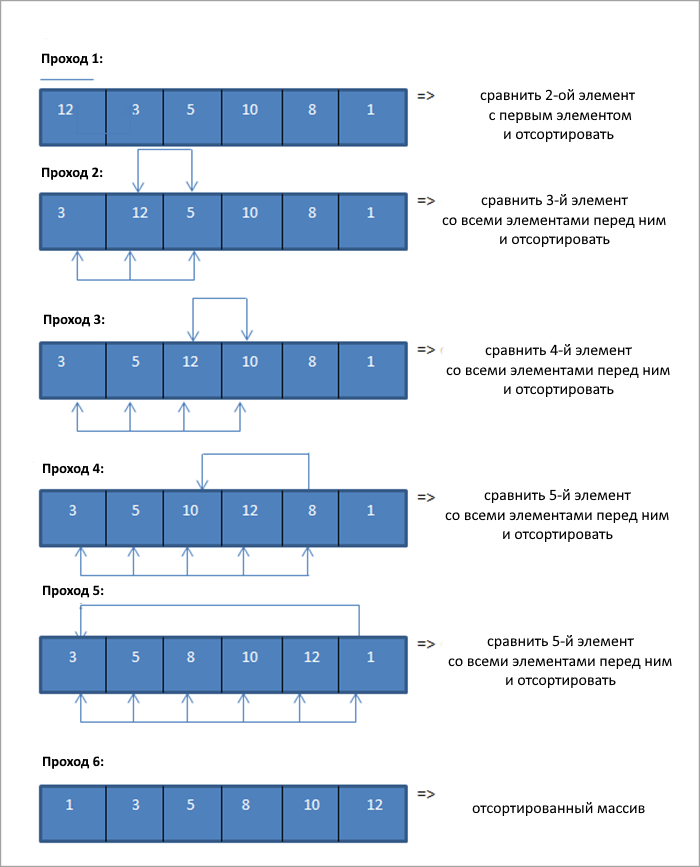
Теперь для каждого прохода мы сравниваем текущий элемент со всеми его предыдущими элементами. Итак, в первом проходе мы начинаем со второго элемента:
Таким образом, нам требуется N проходов, чтобы полностью отсортировать массив, содержащий N элементов.
Приведенную выше демонстрацию можно показать в табличной форме:
| Проход | Несортированный список | Сравнение | Отсортированный список |
| 1 | {12,3,5,10,8,1} | {12,3} | {3,12,5,10,8,1} |
| 2 | {3,12,5,10,8,1} | {3,12,5} | {3,5,12,10,8,1} |
| 3 | {3,5,12,10,8,1} | {3,5,12,10} | {3,5,10,12,8,1} |
| 4 | {3,5,10,12,8,1} | {3,5,10,12,8} | {3,5,8,10,12,1} |
| 5 | {3,5,8,10,12,1} | {3,5,8,10,12,1} | {1,3,5,8,10,12} |
| 6 | {} | {} | {1,3,5,8,10,12} |
Как показано на схеме выше, мы начинаем со второго элемента, так как предполагаем, что первый элемент всегда сортируется. Итак, мы начинаем со сравнения второго элемента с первым и меняем местами, если второй элемент меньше первого.
Этот процесс сравнения и замены помещает два элемента на свои места. Затем мы сравниваем третий элемент с его предыдущими (первым и вторым) элементами и выполняем ту же процедуру, чтобы поместить третий элемент на нужное место.
Таким образом, для каждого прохода мы помещаем один элемент на нужное место. Для первого прохода мы размещаем второй элемент на его месте. Таким образом, в общем случае, чтобы разместить N элементов на своих местах, нам потребуется N-1 проходов.
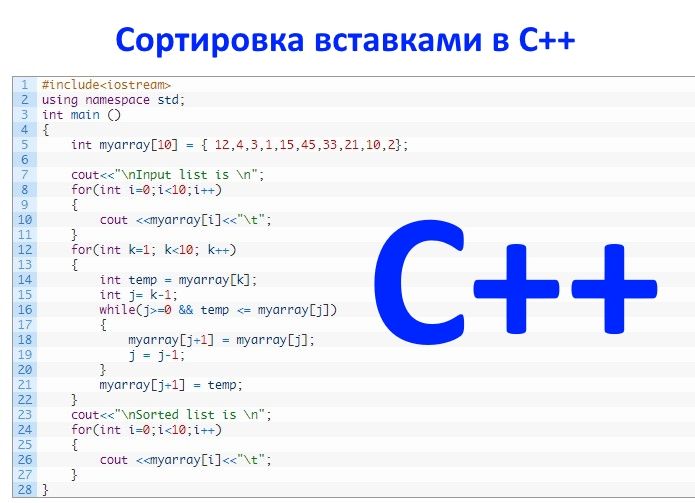
Далее мы продемонстрируем реализацию метода сортировки вставками на языке C++:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
#include<iostream> using namespace std; int main () { int myarray[10] = { 12,4,3,1,15,45,33,21,10,2}; cout<<"\nInput list is \n"; for(int i=0;i<10;i++) { cout <<myarray[i]<<"\t"; } for(int k=1; k<10; k++) { int temp = myarray[k]; int j= k-1; while(j>=0 && temp <= myarray[j]) { myarray[j+1] = myarray[j]; j = j-1; } myarray[j+1] = temp; } cout<<"\nSorted list is \n"; for(int i=0;i<10;i++) { cout <<myarray[i]<<"\t"; } } |
Вывод данных:
| Список ввода 12 4 3 1 15 45 33 21 10 2 Отсортированный список 1 2 3 4 10 12 15 21 33 45 |
Далее мы покажем реализацию метода сортировки вставками в Java:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
public class Main { public static void main(String[] args) { int[] myarray = {12,4,3,1,15,45,33,21,10,2}; System.out.println("Input list of elements ..."); for(int i=0;i<10;i++) { System.out.print(myarray[i] + " "); } for(int k=1; k<10; k++) { int temp = myarray[k]; int j= k-1; while(j>=0 && temp <= myarray[j]) { myarray[j+1] = myarray[j]; j = j-1; } myarray[j+1] = temp; } System.out.println("\nsorted list of elements ..."); for(int i=0;i<10;i++) { System.out.print(myarray[i] + " "); } } } |
Вывод данных:
| Введите список элементов… 12 4 3 1 15 45 33 21 10 2 отсортированный список элементов … 1 2 3 4 10 12 15 21 33 45 |
В обеих реализациях видно, что мы начинаем сортировку со второго элемента массива (переменная цикла j = 1) и многократно сравниваем текущий элемент со всеми его предыдущими элементами, а затем сортируем элемент, чтобы поместить его в нужное место, если текущий элемент не соответствует всем предыдущим элементам.
Сортировка вставками работает лучше всего и может быть выполнена за меньшее количество проходов, если массив частично отсортирован. Но по мере того, как список становится больше, его производительность снижается. Еще одним преимуществом сортировки вставками является то, что это стабильная сортировка, что означает, что она сохраняет порядок одинаковых элементов в списке.
Анализ сложности алгоритма сортировки вставками
Судя по псевдокоду и демонстрации выше, сортировка вставками является более эффективным алгоритмом по сравнению с пузырьковой сортировкой или сортировкой выбором. Вместо цикла for и текущих условий используется цикл while, который не выполняет дополнительных действий при сортировке массива.
Однако, даже если мы передаем отсортированный массив методу сортировки вставками, он все равно будет выполнять внешний цикл for, что потребует n шагов для сортировки уже отсортированного массива. Это делает наилучшую временную сложность сортировки вставками линейной функцией N, где N — количество элементов в массиве.
Таким образом, различные сложности метода сортировки вставками приведены ниже:
| Временная сложность в худшем случае | O(n 2) |
| Временная сложность в лучшем случае | O(n) |
| Средняя временная сложность | O(n 2) |
| Пространственная сложность | O(1) |
Несмотря на эти сложности, мы все же можем заключить, что сортировка вставками является наиболее эффективным алгоритмом по сравнению с другими методами сортировки, такими как пузырьковая сортировка и сортировка выбором.
Итог
Сортировка вставками является наиболее эффективной из всех трех обсуждавшихся до этой статьи методов. Здесь мы предполагаем, что первый элемент отсортирован, а затем многократно сравниваем каждый элемент со всеми его предыдущими элементами, а затем помещаем текущий элемент в нужное место в массиве.
В этой статье при обсуждении сортировки вставками мы указали, что мы сравниваем элементы с шагом 1, а также они являются смежными. Эта функция приводит к тому, что для получения отсортированного списка требуется больше проходов.
В нашей следующей статье мы поговорим о технике сортировки слиянием в C++.
С Уважением, МониторБанк