Блог

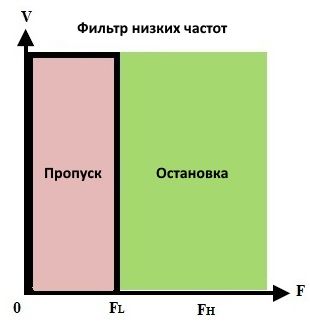
Фильтр низких частот пропускает все частоты от постоянного тока до верхней частоты среза fH и подавляет любые сигналы выше этой частоты.

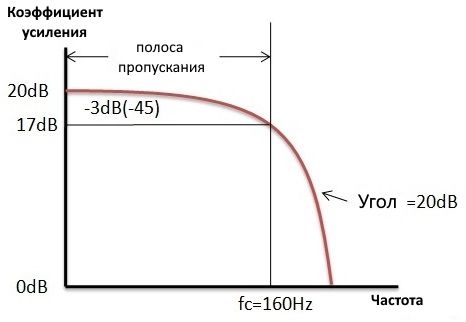
В идеальном случае кривая АЧХ падает на частоте среза. Практически сигнал не будет падать внезапно, а будет постепенно падать от переходной области к области стоп-полосы.

Частота среза — это точка, в которой отклик падает на -3 дБ или 70,7% от полосы пропускания. Переходная область — это область, где происходит спад.

Область полосы задерживания — это область, в которой затухание происходит в основном для входных сигналов.

Активный фильтр низких частот состоит не из одних только пассивных компонентов, а из таких активных компонентов, как операционные усилители, полевые транзисторы и транзисторы в сочетании с пассивными компонентами. Эти фильтры очень эффективны по сравнению с пассивными фильтрами. Активные фильтры вводятся для преодоления недостатков пассивных фильтров.

Простой активный фильтр низких частот формируется с использованием операционного усилителя. Операционный усилитель принимает сигнал с высоким импедансом на вход и выдает сигнал с низким импедансом на выходе. Компонент усилителя в этой схеме фильтра увеличивает амплитуду выходного сигнала.

Благодаря этому действию усилителя выходной сигнал станет шире или уже. Максимальная частотная характеристика фильтра зависит от усилителя, используемого в схемотехнике.

Цепь активного фильтра низких частот

Затухание сигнала, т.е. амплитуда выходного сигнала меньше амплитуды входного сигнала в пассивной цепи. Чтобы преодолеть этот недостаток пассивного фильтра, разработан активный фильтр. Пассивный фильтр низких частот, подключенный либо к инвертирующему, либо к неинвертирующему операционному усилителю, дает нам простой активный фильтр низких частот.

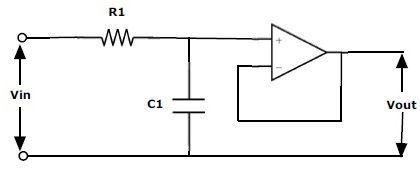
Активный фильтр первого порядка образован одним операционным усилителем с RC-цепочкой. Ниже показан простой пассивный RC-фильтр, подключенный к неинвертирующему выводу операционного усилителя.

Эта RC-цепочка обеспечит низкочастотный тракт на вход усилителя. Усилитель действует как буферная схема, обеспечивающая единичное усиление на выходе. Эта схема имеет большее значение входного сопротивления. Несмотря на то, что входной импеданс операционных усилителей намного ниже частоты среза, этот входной импеданс ограничен последовательным импедансом, равным R+ 1⁄jωC.

Выходное сопротивление операционного усилителя, включенного в схему, всегда низкое. Эта схема обеспечит высокую стабильность фильтра. Основным недостатком этой конфигурации является коэффициент усиления по напряжению, равный единице. Даже для этой схемы выходная мощность высока, поскольку входное сопротивление низкое.

Активный фильтр низких частот с усилением по высокому напряжению

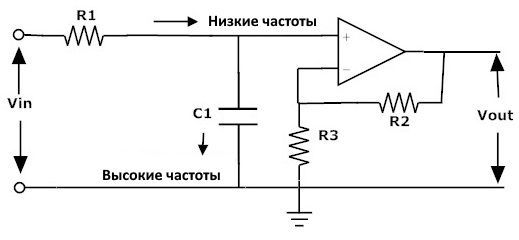
Вышеупомянутая активная схема фильтра низких частот обеспечивает не более чем единичное усиление. Таким образом, мы используем приведенную ниже схему для обеспечения высокого коэффициента усиления по напряжению.

Когда входные сигналы имеют низкую частоту, сигналы проходят через схему усиления напрямую, но если входная частота высока, сигналы проходят через конденсатор C1. С помощью этой схемы фильтра амплитуда выходного сигнала увеличивается за счет усиления полосы пропускания фильтра.

Вы должны знать, что для схемы неинвертирующего усилителя величина коэффициента усиления по напряжению получается путем деления резистора обратной связи R ₂  на соответствующий входной резистор R ₃ .

Вот что получается:

Величина напряжения коэффициента усиления = {1 + (R ₂ /R3)}

Усиление напряжения активного фильтра низких частот

Вы должны помнить, что усиление может быть получено частотными составляющими:

Коэффициент усиления по напряжению = V_out⁄V_in = A_max⁄ √(1+〖f/f_c 〗^2)

Где,

• A _max = усиление полосы пропускания = 1 + R_2⁄R_3
• f = рабочая частота.
• f _c = частота среза.
• V_out  = выходное напряжение.
• V_in = входное напряжение.

При увеличении частоты усиление уменьшается на 20 дБ на каждые 10-кратное увеличение частоты.

На низких частотах, то есть когда рабочая частота f меньше частоты среза, тогда:

V_out / V_in = A_max

Когда рабочая частота равна частоте среза, то

V_out / V_in = A_max / √2 = 0.707 A_max

Если рабочая частота меньше частоты среза, то

V_out / V_in < A_max

По этим уравнениям можно сказать, что на низких частотах коэффициент усиления контура равен максимальному коэффициенту усиления, а на высоких частотах коэффициент усиления контура меньше максимального коэффициента усиления A _max .

Когда фактическая частота равна частоте среза, коэффициент усиления равен 70,7% от A _max . Таким образом, мы можем сказать, что при каждом десятикратном увеличении частоты прирост напряжения делится на 10.

Величина коэффициента усиления по напряжению (дБ): _макс . A = 20 log ₁₀ (В _{на выходе} / В _{на входе} )

При частоте -3 дБ коэффициент усиления определяется как:

3 dB A_max = 20 log₁₀ {0.707 (V_out / V_in)}

Пример активного фильтра низких частот

Рассмотрим неинвертирующий активный фильтр низких частот с частотой среза 160 Гц и входным сопротивлением 15 кОм. Предположим, что на низких частотах эта схема имеет коэффициент усиления по напряжению, равный 10.

Коэффициент усиления в дБ определяется как 20log (A _max ) = 20log (10) = 20 дБ.

Вы наверняка помните, что коэффициент усиления по напряжению определяется как:

А _макс  = 10 = 1 + (R ₂ /R ₁ )

Пусть резистор R ₁  будет 1,2 кОм

R ₂  = 9R ₁  = 9 x 1,2 к = 10,8 кОм

Следовательно, полученное значение R ₂  равно 10,8 кОм. Поскольку этого значения не существует, мы можем рассматривать ближайшее предпочтительное стандартное значение как 11 кОм.

Рассмотрев уравнение частоты среза, мы можем получить значение конденсатора.

f_C = 1/ 2πRC

Рассматривая C как основной, мы можем записать приведенное выше уравнение следующим образом:

C = 1 / 2πf_CR

Замените значение входного импеданса на 15 кОм, значение f_C на 160 Гц.

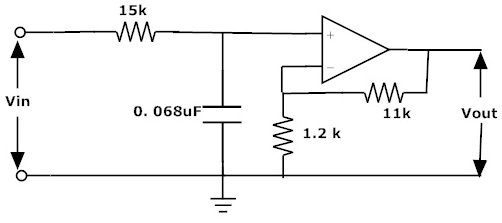
Следовательно, C = 0,068 мкФ.

Из полученных значений мы можем получить активный фильтр низких частот следующим образом:

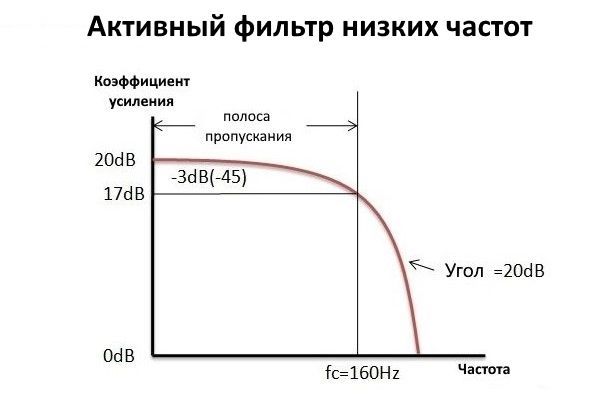
Частотная характеристика

Реакция активного фильтра показана на схеме ниже:

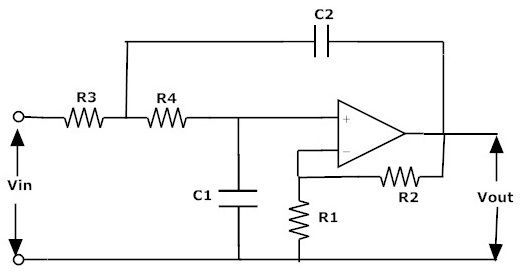
Активный фильтр низких частот второго порядка

Просто добавив дополнительную RC-цепь к фильтру низких частот первого порядка, схема ведет себя как фильтр второго порядка. Схема фильтра второго порядка показана выше.

Коэффициент усиления вышеуказанной схемы составляет A _max  = 1 + (R ₂ /R ₁ ) .

Частота среза фильтра низких частот второго порядка составляет f _c = 1 / 2π√(C ₁ C ₂ R ₃ R ₄ )

Частотная характеристика и этапы проектирования фильтров второго порядка и фильтров первого порядка почти одинаковы, за исключением спада полосы задерживания. Значение спада фильтра второго порядка вдвое больше, чем у фильтра первого порядка, которое составляет 40 дБ или 12 дБ. Эти фильтры останавливают высокочастотные сигналы с более крутым уклоном.

Итог

В электронике эти фильтры широко используются во многих областях. Эти фильтры используются в качестве фильтров в аудиодинамиках для уменьшения высокочастотного шипения, производимого в системе, и используются в качестве входов для сабвуферов. Они также используются в эквалайзерах и аудиоусилителях.

При аналого-цифровом преобразовании фильтры используются в качестве сглаживающих фильтров для управления сигналами. В цифровых фильтрах они используются для размытия изображений, сглаживания наборов сигналов данных. В радиопередатчиках для блокировки гармонических излучений. А в акустике эти фильтры используются для фильтрации высокочастотных сигналов из передаваемого звука, которые вызывают эхо на более высоких звуковых частотах.

В следующей статье мы поговорим об активном фильтре высоких частот.

С Уважением, МониторБанк