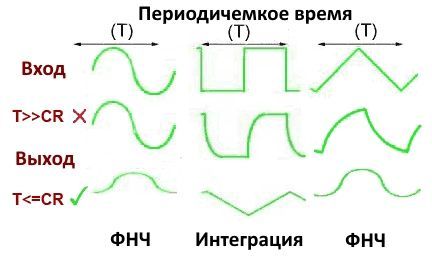
Интеграция широко используется в электронике для преобразования прямоугольных сигналов в треугольные формы, при этом она имеет эффект, противоположный дифференцированию (описанный в статье «Дифференциаторы»). Форма входной волны схемы интегратора в этом случае будет графиком скорости изменения выходной волны, что можно увидеть, сравнивая форму входного и выходного сигналов прямоугольной формы на картинке ниже.
| Серия статей по фильтрам |
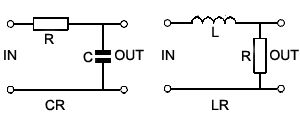
Обратите внимание, что схема интегратора (показанная на рис. 8.5.1) представляет собой схему фильтра низких частот CR, описанного в статье «Работа фильтров».
Действие интегратора с синусоидальным входом
Если вход представляет собой синусоидальную волну, схема действует не как интегратор, а как простой фильтр низких частот (ФНЧ), в котором амплитуда выходной волны уменьшена, а ее фаза относительно входной волны сдвинута так, что запаздывает до -90° в зависимости от частоты волны и постоянной времени CR цепи.
Таким образом, схема фильтра низких частот называется интегратором только в том случае, если:
- входная волна представляет собой прямоугольную волну.
- периодическое время (T) входной волны намного короче, чем постоянная времени цепи (CR) , т.е. (T<=CR).
При соблюдении этих условий действие интегратора противоположно действию схемы дифференциатора.
Интеграция прямоугольной волны
Диаграмма ниже показывает, что при входном сигнале прямоугольной формы и правильном соотношении между периодическим временем волны и постоянной времени цепи происходит интегрирование. На выходе теперь (рассматривая формы волны как простые графики) график изменения площади под входной волной. Интегратор преобразовал прямоугольную волну на входе в треугольную волну на выходе, наклон этой волны описывает увеличение площади под прямоугольной волной (движение слева направо).
Чтобы схема эффективно действовала как интегратор, периодическое время волны должно быть равно или меньше постоянной времени цепи, т.е. (T<=CR). Чем выше частота входной волны для конкретной постоянной времени, тем лучше будет форма выходной волны, но меньше ее амплитуда. Также обратите внимание, что, в отличие от дифференциатора, интегратор не блокирует какую-либо постоянную составляющую входной волны. Следовательно, выходная волна с уменьшенной амплитудой будет иметь постоянную составляющую, которая (без учета сопротивления любой нагрузки на выходе) будет такой же, как средний уровень постоянного тока входной волны.
На более низких частотах, где периодическое время T волны намного больше, чем постоянная времени цепи CR (T>>CR), происходит некоторое изменение формы волны, но выходной сигнал не соответствует определению интегратора; схема закруглила быстрые вертикальные переходы прямоугольной волны. Выходной сигнал на этих низких частотах не является графиком изменения площади под входной волной, схема действует как фильтр низких частот и удаляет высокочастотные компоненты прямоугольной волны, которые были ответственны за быстрые вертикальные изменения в каждом полупериоде.
Действие на треугольной волне
Когда входной сигнал схемы интегратора представляет собой треугольную волну, выходной сигнал становится синусоидальным. Помните, однако, что схема интегратора также является фильтром низких частот, который удаляет высокочастотные гармоники, присутствующие в комплексной (треугольной) волне на его входе, оставляя только основную (синусоидальную волну) и, возможно, несколько низкочастотных гармоник. Таким образом, на низких частотах выход схемы интегратора представляет собой закругленную форму треугольной входной волны.
Основная цель пассивного интегратора CR — получить хорошую треугольную форму волны из прямоугольного входного сигнала, что он может сделать очень хорошо и с очень низкими затратами (необходимы только два компонента), хотя выходной сигнал будет уменьшен по амплитуде. Любой недостаток амплитуды можно преодолеть, объединив пассивные схемы CR, описанные в этом модуле, с операционным усилителем для создания активного фильтра, дифференциатора или интегратора.
Для закрепления пройденного материала пройдите наш тест.
С Уважением, МониторБанк